Cho hình chóp đều S.ABCDS.ABCD có SA=2a,AB=3aSA=2a,AB=3a. Tính góc gi
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp đều S.ABCDS.ABCD có SA=2a,AB=3aSA=2a,AB=3a. Tính góc giữa SASA và mặt phẳng đáy ABCABC
Đáp án án đúng là: A
Lời giải chi tiết:
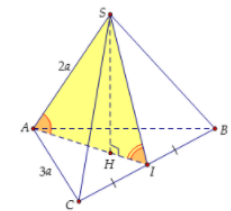
Gọi HH là hình chiếu vuông góc của SS trên (ABC)(ABC).
Do S.ABCS.ABC là hình chóp đều nên HH là trọng tâm tam giác ABCABC (△ABC△ABC đều nên trọng tâm, trực tâm, tâm đường tròn ngoại tiếp, nội tiếp của tam giác ABCABC trùng nhau) (1)
Ta có: SH⊥(ABC)SH⊥(ABC)
⇒^(SA;(ABC))=^(SA;HA)=^SAH⇒ˆ(SA;(ABC))=ˆ(SA;HA)=ˆSAH
Gọi II là trung điểm của BCBC, khi đó tam giác ABCABC đều cạnh 3a3a nên:
AI=3a√32⇒AH=23AI=a√3AI=3a√32⇒AH=23AI=a√3
Xét tam giác SAHSAH ta có:
cos^SAH=AHSA=a√32a=√32⇒^SAH=30∘cosˆSAH=AHSA=a√32a=√32⇒ˆSAH=30∘
Vậy ^(SA;(ABC))=30∘ˆ(SA;(ABC))=30∘
Đáp án A
Xem thêm các bài tiếp theo bên dưới