Cho hình chóp A.BCD có cạnh $\large AC\perp (BCD)$ và BCD là tam giác

Cho hình chóp A.BCD có cạnh $\large AC\perp (BCD)$ và BCD là tam giác đều cạnh bằng a. Biết $\large AC=a\sqrt{2}$, khoảng cách từ A đến đường thẳng BD bằng: 

• A. $\large \dfrac{3a\sqrt{2}}{2}$
• B. $\large \dfrac{2a\sqrt{3}}{3}$
• C. $\large \dfrac{4a\sqrt{5}}{3}$
• D. $\large \dfrac{a\sqrt{11}}{2}$

Chọn D

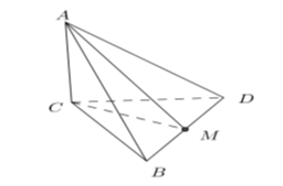
Gọi M là trung điểm của BD
Ta có: $\large \left\{\begin{align}& AC\perp BD\\& CM\perp BD\\\end{align}\right. $ $\large \Rightarrow  BD\perp AM$ (Định lý ba đường vuông góc) $\large \Rightarrow  d(A,BD)= AM$
$\large CM= \dfrac{a\sqrt{3}}{2}$ (vì tam giác BCD đều)
Ta có: $\large AM= \sqrt{AC^2+MC^2}= \sqrt{2a^2+\dfrac{3a^2}{4}}= \dfrac{a\sqrt{11}}{2}$