Cho hàm số y=f(x) xác định trên $\large \mathbb{R} \backslash\{0\}$, l

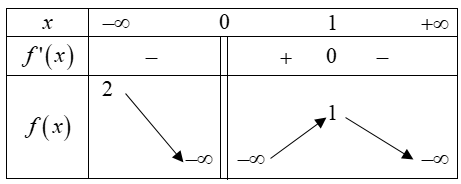
Cho hàm số y=f(x) xác định trên $\large \mathbb{R} \backslash\{0\}$, liên tục trên mỗi khoảng khác định và có bảng biến thiên như sau

Tìm tất cả giá trị thực của tham số m để phương trình $\large |f(x)|=m$ có 4 nghiệm phân biệt.

• A.

  A. $\large m \geq 2$

• B.

  B. $\large 0

• C.

  C. $\large 1

• D.

  D. $\large 0< m<1$

Ta có bảng biến thiên của hàm số $\Large y=|f(x)|$

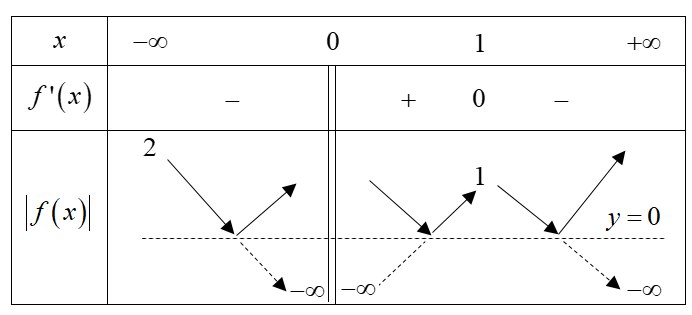
Xét phương trình $\large |f(x)|=m$

Nếu m<0: phương trình vô nghiệm.

Nếu m=0: phương trình tương đương f(x)=0 có 3 nghiệm.

Nếu m>0: phương trình tương đương f(x)=m hoặc f(x)=-m.

- Với 0

- Với m=1: phương tình f(x)=-m có 3 nghiệm, phương trình f(x)=m có 2 nghiệm. Tổng cộng phương trình ban đầu có 5 nghiệm.

- Với 1

- Với $\large m \geq 2$: phương tình f(x)=-m có 3 nghiệm, phương trình f(x)=m vô nghiệm. Tổng cộng phương trình ban đầu có 3 nghiệm.

Vậy 1