Cho hàm số $y=f(x)$. Hàm số $y=f'(x)$ có đồ thị trên một khoảng K như

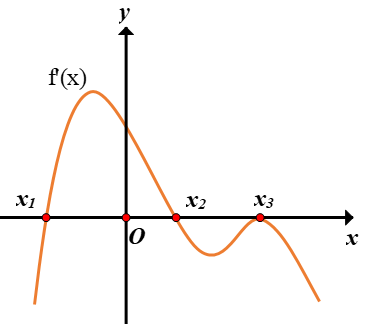
Cho hàm số $y=f(x)$. Hàm số $y=f'(x)$ có đồ thị trên một khoảng K như hình vẽ bên. Trong các khẳng định sau, có tất cả bao nhiêu khẳng định sai?

(I). Trên K, hàm số $y=f(x)$ có hai điểm cực trị.

(II). Hàm số $y=f(x)$ đạt cực đại tại $\large x_{3}$.

(III). Hàm số $y=f(x)$ đạt cực tiểu tại $\large x_{1}$.

• A.

  A. 3

• B.

  B. 0

• C.

  C. 1

• D.

  D. 2

Từ đồ thị hàm số suy ra bảng biến thiên

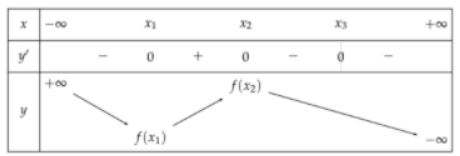
Khẳng định (I) đúng vì trên khoảng K, hàm số có 2 điểm cực trị.

Khẳng định (II) sai vì $\large x=x_{3}$ không phải là điểm cực trị của hàm số.

Khẳng định (III) đúng vì hàm số đạt cực tiểu tại $\large x=x_{1}$.

Chọn đáp án C.