Cho hàm số $\large y=\dfrac{x^{2}+m x+1}{x+m}$ (m là tham số). Tìm tất

Cho hàm số $\large y=\dfrac{x^{2}+m x+1}{x+m}$ (m là tham số). Tìm tất cả các giá trị của tham số m để hàm số có giá trị cực đại là 7.

• A.

  A. m=7.

• B.

  B. m=5.

• C.

  C. m=-9.

• D.

  D. m=-5.

Điều kiện $\large x \neq-m$. Đạo hàm: $\large y^{\prime}=\dfrac{x^{2}+2 m x+m^{2}-1}{(x+m)^{2}}=\dfrac{(x+m)^{2}-1}{(x+m)^{2}}, y^{\prime}=0 \Leftrightarrow\left[\begin{array}{l}
x=1-m \\
x=-1-m
\end{array}\right.$.
Vì $\large 1-m \neq-1-m, \forall m \in \mathbb{R}$ nên hàm số luôn có hai điểm cực trị $\large \forall m \in \mathbb{R}$
Phương trình đường thẳng qua hai điểm cực trị của đồ thị là $\large y=2 x+m$.
Suy ra $\large y(1-m)=2-m, y(-1-m)=-2-m$.(Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y=\dfrac{ax^2+bx+c}{mx+n} là y=\dfrac{ax+b}{m})
Ta có bảng biến thiên:

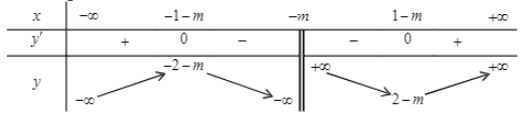
Ta có $\large y_{C Đ}=-2-m=7 \Leftrightarrow m=-9$. Chọn C.