Cho hàm số $y=f(x)$ có đạo hàm trên $\large \mathbb{R}$. Đồ thị hàm số

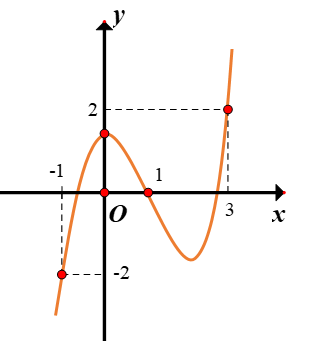
Cho hàm số $y=f(x)$ có đạo hàm trên $\large \mathbb{R}$. Đồ thị hàm số $\large y=f^{\prime}(x)$ như hình vẽ. Tìm các khoảng đơn điệu của hàm số $\large g(x)=2 f(x)-x^{2}+2 x+2017$

Mệnh đề nào dưới đây đúng?

• A.

  A. Hàm số g(x) nghịch biến trên (1;3).

• B.

  B. hàm số g(x) có 2 điểm cực trị đại.

• C.

  C. Hàm số g(x) đồng biến trên (-1;1).

• D.

  D. Hàm số g(x) nghịch biến trên $\large (3 ;+\infty)$.

Chọn C. Ta có $\large g^{\prime}(x)=2 f^{\prime}(x)-2 x+2=2\left[f^{\prime}(x)-(x-1)\right]$

Dựa vào hình vẽ ta thấy đường thăng y=x-1 cắt đồ thị hàm số $\large y=f'(x)$ tại 3 điểm: $\large (-1 ;-2),(1 ; 0),(3 ; 2)$.

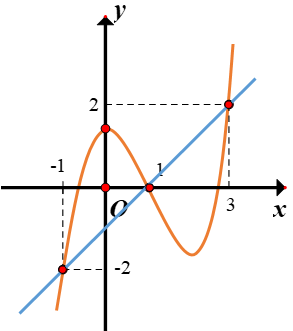
Dựa vào đồ thị ta có $\large g^{\prime}(x)=0 \Leftrightarrow 2[f '(x)-(x-1)]<0$ $\large \Leftrightarrow\left[\begin{array}{l}
x=-1 \\
x=1 \\
x=3
\end{array}, g'(x)>0\right.$ $\large \Leftrightarrow 2\left[f^{\prime}(x)-(x-1)\right]>0$ $\large \Leftrightarrow\left[\begin{array}{l}
1- 3 \end{array}\right.$ $\large g^{\prime}(x)<0 \Leftrightarrow$ $\large 2\left[f^{\prime}(x)-(x-1)\right]<0 \Leftrightarrow\left[\begin{array}{l}
x<-1 \\
1 \end{array}\right.$

Ta có bảng xét dấu:

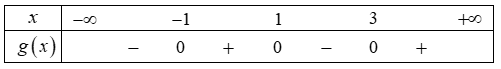
Vậy hàm số y=g(x) đồng biến trên các khoảng (-1;1).