Cho hàm số $\large y=x^{4}-2 x^{2}+1$ có đồ thị như hình vẽ. Có bao nh

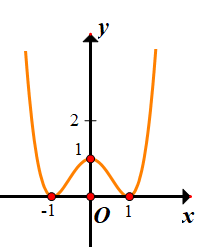
Cho hàm số $\large y=x^{4}-2 x^{2}+1$ có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m sao cho phương trình $\large x^{4}-2 x^{2}+2-m=0$ có 4 nghiệm thực phân biệt.

• A.

  A. $\large -2$

• B.

  B. $\large 2$

• C.

  C. $\large 0$

• D.

  D. $\large 1$

Phương trình đã cho tương đương với $\large x^{4}-2 x^{2}+1=m-1$. Số nghiệm của phương trình là số giao điểm của đồ thị hàm số $\large y=x^{4}-2 x^{2}+1$ và đường thẳng $\large =m-1$.

Nếu $\large m-1<0 \Leftrightarrow m<1$: phương trình vô nghiệm.

Nếu $\large  m-1=0 \Leftrightarrow m=1$: phương trình có 2 nghiệm.

Nếu $\large 0

Nếu $\large m-1=1 \Leftrightarrow m=2$: phương trình có 3 nghiệm.

Nếu $\large m-1>1 \Leftrightarrow m>2$: phương trình có 2 nghiệm.

Suy ra để phương trình đã cho có 4 nghiệm thực phân biệt thì  1

Mặt khác $\Large m\in \mathbb{Z}$

Vậy không tồn tại giá trị của m thỏa mãn yêu câu bài toán.

Đáp án đúng: C