Cho hàm số y=f(x) có $\large f^{\prime}(x)=x^{2}(x-1)^{2}(x-3)$. Hàm s

Cho hàm số y=f(x) có $\large f^{\prime}(x)=x^{2}(x-1)^{2}(x-3)$. Hàm số $\large g(x)=f(x)+\dfrac{1}{3} x^{3}-5$ đồng biến trên khoảng nào trong các khoảng dưới đây?

• A.

  A. $\Large (0;2)$

• B.

  B. $\large \left(2 ; \dfrac{3+\sqrt{5}}{2}\right)$

• C.

  C. $\large \left(\dfrac{3-\sqrt{5}}{2} ; 2\right)$

• D.

  D. $\large \left(0 ; \dfrac{3-\sqrt{5}}{2}\right)$

Chọn C

Ta có: $\large g^{\prime}(x)=f^{\prime}(x)+x^{2}$

$\large g^{\prime}(x)=0 \Leftrightarrow x^{2}(x-1)^{2}(x-3)=-x^{2}$

$\large \Leftrightarrow\left[\begin{array}{l}
x=0 \\
(x-1)^{2}(x-3)=-1
\end{array} \Leftrightarrow\left[\begin{array}{l}
x=0 \\
x^{2}-5 x^{2}+7 x-2=0
\end{array}\right.\right.$ $\large \Leftrightarrow\left[\begin{array}{l}
x=0 \\
x=2 \\
x=\dfrac{3 \pm \sqrt{5}}{2}
\end{array}\right.$

Ta có bảng xét dấu của g'(x):

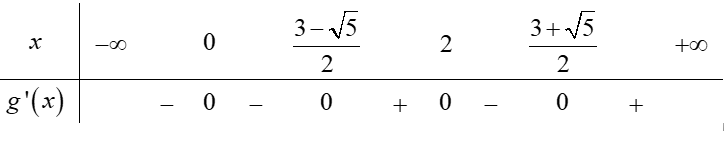
Dựa vào bảng xét dấu g'(x) ta thấy trên khoảng $\large \left(\dfrac{3-\sqrt{5}}{2} ; 2\right)$ thì hàm số y=g(x) đồng biến.