Cho hàm số $y=f(x)$ có đạo hàm và liên tục trên $\large \mathbb{R}$. B

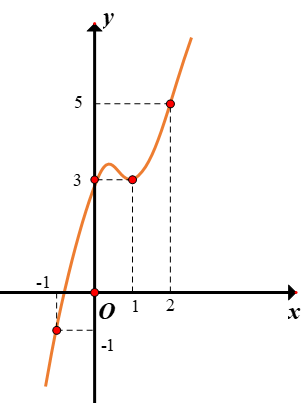
Cho hàm số $y=f(x)$ có đạo hàm và liên tục trên $\large \mathbb{R}$. Biết rằng đồ thị hàm số $y=f'(x)$ như dưới đây.

Cho hàm số $\Large g(x)=f(x)-x^2-x$. Khẳng định nào sau đây ĐÚNG?

• A.

  A. $\large g(-1)>g(1)$

• B.

  B. $\large g(-1)=g(1)$

• C.

  C. $\large g(1)=g(2)$

• D.

  D. $\large g (1) >g(2)$

Chọn D

Ta có $\large g^{\prime}(x)=f^{\prime}(x)-2 x-1$

$g'(x)=0\Leftrightarrowf'(x)=2x+1$

Ta thấy đường thẳng y = 2x + 1 là đường thẳng đi qua các điểm A(-1;-1), B(1;3), C(2;5).

Từ đồ thị hàm số $\large y=f^{\prime}(x)$ và đường thẳng $\large y=2 x+1$ ta có bảng biến thiên:

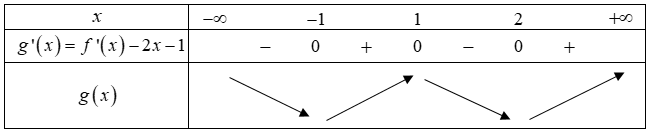
Suy ra đáp án đúng là D.