Cho hàm số y=f(x) có đạo hàm trên $\large \mathbb{R}$. Đồ thị hàm số $

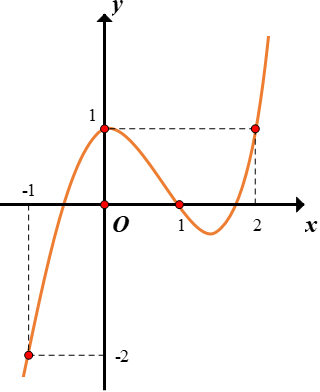
Cho hàm số y=f(x) có đạo hàm trên $\large \mathbb{R}$. Đồ thị hàm số $\large y=f^{\prime}(x)$ như hình vẽ bên dưới.

Hàm số $\large g(x)=f(x)-\dfrac{x^{3}}{3}+x^{2}-x+2$ đồng biến trên khoảng nào trong các khoảng sau?

• A.

  A. (-1;0)

• B.

  B. (0;2)

• C.

  C. (1;2)

• D.

  D. (0;1)

Chọn D

Ta có $\large g^{\prime}(x)=f^{\prime}(x)-x^{2}+2 x-1, g^{\prime}(x)=0 \Leftrightarrow f^{\prime}(x)=(x-1)^{2}$.

Suy ra số nghiệm của phương trình $\large g^{\prime}(x)=0$ chính là số giao điểm giữa đồ thị hàm số $\large f^{\prime}(x)=0$ và parabol $\large (P): y=(x-1)^{2}$.

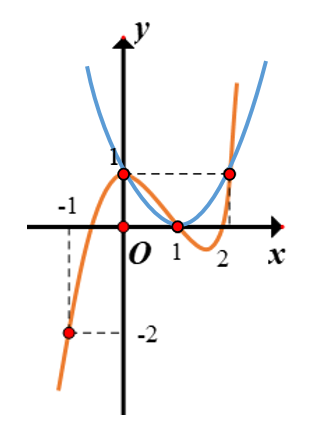
Dựa vào đồ thị ta suy ra $\large g^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l} x=0 \\ x=1 \\ x=2 \end{array}\right.$.

Bảng biến thiên 

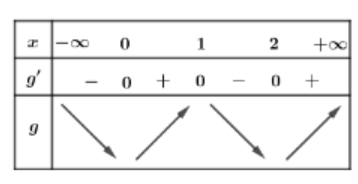
Dựa vào bảng biến thiên và đối chiếu với các đáp án suy ra hàm số đồng biến trên $\Large (0;1)$

 Đáp án đúng: D.