Cho hàm số y=f(x) có đạo hàm trên $\large \mathbb{R}$ có đồ thị $\larg

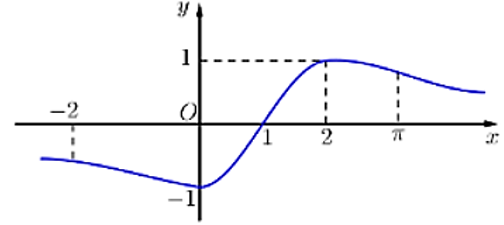
Cho hàm số y=f(x) có đạo hàm trên $\large \mathbb{R}$ có đồ thị $\large f^{\prime}(x)$ như hình vẽ.

Bất phương trình $\large f(x)>\sin \dfrac{\pi x}{2}+m$ nghiệm đúng với mọi $\large x \in[-1 ; 3]$ khi và chỉ khi

 

• A.

  A. $\large m < f(0)$

• B.

  B. $\large m

• C.

  C. $\large m

• D.

  D. $\large m

Chọn đáp án B

$\large f(x)>\sin \dfrac{\pi x}{2}+m \Leftrightarrow m

Để bất phương trình nghiệm đúng với mọi $\large x \in[-1 ; 3]$ thì $\large m<\min _{[-1;3]}\left(f(x)-\sin \dfrac{\pi x}{2}\right)$

Xét hàm số $\large g(x)=f(x)-\sin \dfrac{\pi x}{2}, g^{\prime}(x)=f^{\prime}(x)-\dfrac{\pi}{2} \cos \dfrac{\pi x}{2}$

Nhận thấy $\large f^{\prime}(x)$ đổi dấu khi qua x=1 gợi ý cho ta xét dấu của hàm $\large g^{\prime}(x)$ trên 2 khoảng (-1;1) và (1;3)

Với $\large x \in(-1 ; 1)$ thì $\large \forall x \in(-1 ; 1) \Rightarrow f^{\prime}(x)<0$ (đồ thị hàm số $\large f^{\prime}(x)$ nằm dưới trục hoành)

$\large x \in(-1 ; 1) \Rightarrow \dfrac{\pi x}{2} \in\left(\dfrac{-\pi}{2} ; \dfrac{\pi}{2}\right) \Rightarrow-\dfrac{\pi}{2} \cos \left(\dfrac{\pi x}{2}\right)<0, \forall x \in(-1 ; 1)$

Vậy $\large g^{\prime}(x)=f^{\prime}(x)-\dfrac{\pi}{2} \cos \left(\dfrac{\pi x}{2}\right)<0, \forall x \in(-1 ; 1)$

Với x=1, ta có: $\large g^{\prime}(1)=f^{\prime}(1)-\dfrac{\pi}{2} \cos \left(\dfrac{\pi \cdot 1}{2}\right)=0$

Với $\large x \in(1 ; 3)$, ta có: $\large \forall x \in(1 ; 3) \Rightarrow f^{\prime}(x)>0$ (đồ thị hàm số $\large f^{\prime}(x)$ nằm trên trục hoảnh)

$\large x \in(1 ; 3) \Rightarrow \dfrac{\pi x}{2} \in\left(\dfrac{\pi}{2} ; \dfrac{3 \pi}{2}\right) \Rightarrow-\dfrac{\pi}{2} \cos \left(\dfrac{\pi x}{2}\right)>0, \forall x \in(1 ; 3)$

Vậy $\large g^{\prime}(x)=f^{\prime \prime}(x)-\dfrac{\pi}{2} \cos \left(\dfrac{\pi x}{2}\right)>0, \forall x \in(1 ; 3)$

Ta có bảng biến thiên

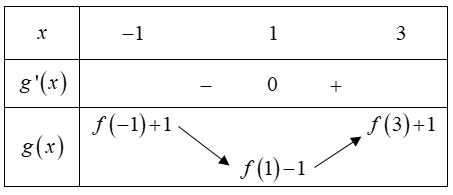
Suy ra $\large \underset{[-1 ; 1]}{\operatorname{Min} g(x)}=f(1)-1$. Vậy $\large m