Cho hàm số y=f(x). Biết rằng hàm số $\large y=f^{\prime}(x)$ có đồ thị

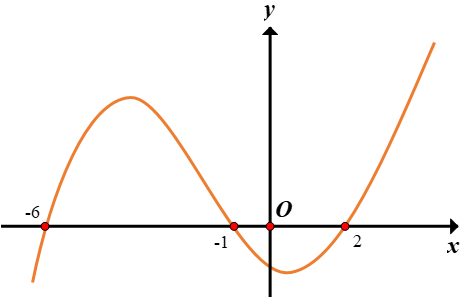
Cho hàm số y=f(x). Biết rằng hàm số $\large y=f^{\prime}(x)$ có đồ thị như hình vẽ bên dưới.

Hàm số $\large y=f\left(3-x^{2}\right)$ đồng biến trên khoảng

• A.

  A. (0;1)

• B.

  B. (-1;0)

• C.

  C. (2;3)

• D.

  D. (-2;-1)

Chọn B

Ta có: $\large y'= \left[f\left(3-x^{2}\right)\right]^{\prime}=0 \Leftrightarrow f^{\prime}\left(3-x^{2}\right) \cdot(-2 x)=0\Leftrightarrow\left[\begin{array}{l} x=0 \\ f^{\prime}(3-x^{2})=0 \end{array}\right.$

Từ đồ thị hàm số suy ra 

$\large f^{\prime}\left(3-x^{2}\right)=0 \Leftrightarrow\left[\begin{array}{l}
3-x^{2}=-6 \\
3-x^{2}=-1 \\
3-x^{2}=2
\end{array} \Leftrightarrow\left[\begin{array}{l}
x=\pm 3 \\
x=\pm 2\\

x=\pm 1
\end{array}\right.\right.$

$\Large f'\left( 3-{{x}^{2}} \right)>0\Leftrightarrow \left[ \begin{matrix}  & -6<3-{{x}^{2}}<-1 \\  & 3-{{x}^{2}}>2 \\ \end{matrix} \right.$$\Large \Leftrightarrow \left[ \begin{matrix}  & 9>{{x}^{2}}>4 \\  & {{x}^{2}}<1 \\ \end{matrix} \right.$$\Large \Leftrightarrow \left[ \begin{matrix}  & -3

$\Large f'\left( 3-{{x}^{2}} \right)<0\Leftrightarrow \left[ \begin{matrix}  & 3-{{x}^{2}}<-6 \\  & -1<3-{{x}^{2}}<2 \\ \end{matrix} \right.$$\Large \Leftrightarrow \left[ \begin{matrix}  & {{x}^{2}}>9 \\  & 1<{{x}^{2}}<4 \\ \end{matrix} \right.$$\Large \Leftrightarrow \left[ \begin{matrix}  & x>3 \\  & x<-3 \\  & -2

Bảng biến thiên

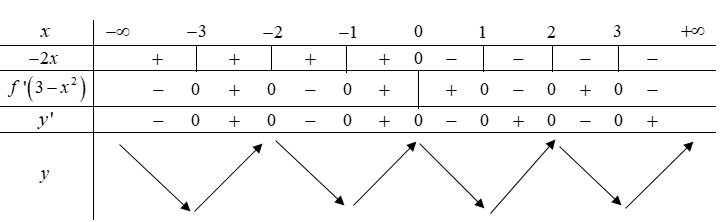
Từ bảng biến thiên của hàm số $\large y=f\left(3-x^{2}\right)$ ta được hàm số đồng biến trên (-1;0).