Cho hàm số $\Large y=x^3-3x+m+1$ có đồ thị là (C). Giá trị của $\Large

Cho hàm số $\Large y=x^3-3x+m+1$ có đồ thị là (C). Giá trị của $\Large m$ để đồ thị (C) cắt trục hoành tại ba điểm phân biệt là:

• A.

  $\Large -1\leq m\leq 3$.

• B.

  $\Large -1 < m < 3$.

• C.

  $\Large m\geq -3$.

• D.

  $\Large -3 < m < 1$.

Chọn D

Phương trình hoành độ giao điểm của (C) và trục hoành là:

$\Large x^3-3x+m+1=0$ $\Large \Leftrightarrow m+1=-x^3+3x=f(x)$ $\Large f'(x)=-3x^2+3=0$ $\Large \Rightarrow x=\pm 1$

BBT: 

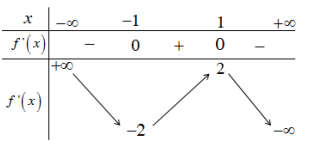
Từ BBT suy ra: Đồ thị (C) cắt trục hoành tại ba điểm phân biệt khi và chỉ khi

$\Large y_{CT} < m+1 < y_{CD}$ $\Large \Leftrightarrow -2 < m+1 < 2$ $\Large \Leftrightarrow -3 < m < 1$.