Cho hàm số $\Large y=f(x)$ là hàm số bậc ba có đồ thị như hình vẽ bên.
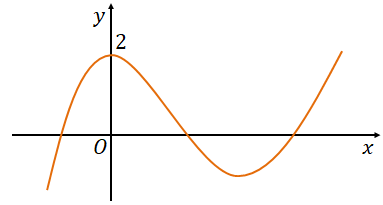
MỤC LỤC
Câu hỏi:
Cho hàm số $\Large y=f(x)$ là hàm số bậc ba có đồ thị như hình vẽ bên. Biết $\Large \int\limits_{1}^{4}{x.{f}''(x-1)dx=7}$ và $\Large \int\limits_{1}^{2}{2x.{f}'({{x}^{2}}-1)dx=-3}$. Phương trình tiếp tuyến với đồ thị hàm số $\Large y=f(x)$ tại điểm có hoành độ $\Large x=3$ là
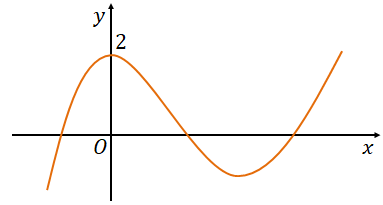
Đáp án án đúng là: A
Lời giải chi tiết:
Từ đồ thị hàm số suy ra $\Large f(0)=2$ và $\Large {f}'(0)=0$
Xét $\Large \int\limits_{1}^{2}{2x.{f}'({{x}^{2}}-1)dx=-3}$ . Đặt $\Large u={{x}^{2}}-1$ $\Large \Rightarrow du=2xdx$
Đổi cận: $\Large x=1\Rightarrow u=0;x=2\Rightarrow u=3$ . Ta có $\Large \int\limits_{0}^{3}{{f}'(u)du=f(u)\left| \begin{align} & 3 \\ & 0 \\ \end{align} \right.=-3}$ $\Large \Leftrightarrow f(3)-f(0)=-3\Leftrightarrow f(3)=-1$
Xét $\Large \int\limits_{1}^{4}{x.{f}''(x-1)dx=7}$. Đặt $\Large u=x-1\Rightarrow x=u+1\Rightarrow du=dx$
Đổi cận $\Large x=1\Rightarrow u=0;x=4\Rightarrow u=3$
$\Large \Rightarrow \int\limits_{0}^{3}{(u+1){f}''(u)du=\int\limits_{0}^{3}{(u+1)d{f}'(u)=}}$ $\Large (u+1){f}'(x)\left| \begin{align} & 3 \\ & 0 \\ \end{align} \right.-\int\limits_{0}^{3}{{f}'(u)du}$
$\Large =4{f}'(3)-{f}'(0)-f(u)\left| \begin{align} & 3 \\ & 0 \\ \end{align} \right.$ $\Large =4{f}'(3)-{f}'(0)-f(3)+f(0)=7$
$\Large \Leftrightarrow 4{f}'(3)=7+f(3)-f(0)=4\Leftrightarrow {f}'(3)=1$
$\Large \Rightarrow $ Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ $\Large x=3$ là $\Large y=f'(3)(x-3)+f(3)=x-4$
Chọn đáp án A
Xem thêm các bài tiếp theo bên dưới
- Cho hàm số $\Large f(x)$ liên tục trên $\Large R$ thỏa mãn $\Large \in
- Cho hai nửa đường tròn như hình vẽ bên dưới , trong đó đường kính của
- Họ nguyên hàm của hàm số $\Large y=f(x)={{x}^{2}}-2x+1$ là $\Large F(x
- Cho hàm số $\Large y={{\pi }^{x}}$ có đồ thị $\Large (C)$ . Gọi $\Larg
- Cho hàm số $\Large y=f(x)$ liên tục trên [a;b], có đồ thị $\Large y={f