Cho hai nửa đường tròn như hình vẽ bên dưới , trong đó đường kính của

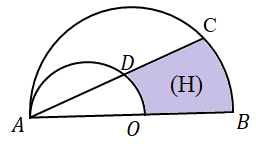
Cho hai nửa đường tròn như hình vẽ bên dưới , trong đó đường kính của nửa đường tròn lớn gấp đôi đường kính của đường tròn nhỏ . Biết rằng nửa hình tròn đường kính AB có diện tích là $\Large 32\pi$ và góc $\Large \widehat{BAC}={{30}^{\circ}}$ . Tính thể tích của vật thể tròn xoay được tạo thành khi quay hình $\Large (H)$ ( phần gạch sọc trong hình vẽ ) xung quanh đường thẳng AB 

• A.

  $\Large 279\pi $

• B.

  $\Large \dfrac{620\pi }{3}$

• C.

  $\Large \dfrac{784\pi }{3}$

• D.

  $\Large \dfrac{325\pi }{3}$

Đặt AB=2R. Ta được: $\Large \dfrac{\pi {{R}^{2}}}{2}=32\pi \Rightarrow {{R}^{2}}=64\Rightarrow R=8$

Xét hệ trục tọa độ $\Large Oxy$ với gốc tọa độ $\Large O$ trùng khớp với tâm đường tròn lớn  $\Large A(-8;0)$, $\Large B(8;0)$

Phương trình đường tròn lớn là: $\Large ({{C}_{1}}):{{x}^{2}}+{{y}^{2}}=64$

Phương trình đường tròn nhỏ là: $\Large ({{C}_{2}}):{{(x+4)}^{2}}+{{y}^{2}}=16$

Đường thẳng AC đi qua điểm $\Large A(-8;0)$ , hệ số góc $\Large k=\tan {{30}^{\circ }}=\dfrac{\sqrt{3}}{3}$ có phương trình là $\Large y=\dfrac{\sqrt{3}}{3}(x+8)$

Tọa độ các điểm $\Large C(4;4\sqrt{3}),D(-2;2\sqrt{3})$

Thể tích khối tròn xoay khi xoay xung quanh trục AB phần tam giác cong ABC là 

$\Large {{V}_{1}}=\pi \left( \int\limits_{-8}^{4}{\dfrac{1}{3}{{(x+8)}^{2}}dx+\int\limits_{4}^{8}{(64-{{x}^{2}}}})dx \right)=\dfrac{896\pi }{3}$

Thể tích khối tròn xoay khi xoay xung quanh trục AB phần tam giác cong AOD là

$\Large {{V}_{2}}=\pi \left( \int\limits_{-8}^{-2}{\dfrac{1}{3}{{(x+8)}^{2}}dx+\int\limits_{-2}^{0}{16-{{(x+4)}^{2}}dx}} \right)=\dfrac{112\pi }{3}$

Vậy thể tích khối tròn xoay cần tìm là 

$\Large V={{V}_{1}}-{{V}_{2}}=\dfrac{896\pi }{3}-\dfrac{112\pi }{3}=\dfrac{784\pi }{3}$

Chọn đáp án C