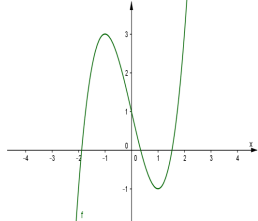
Cho hàm số y=f(x) có đồ thị hàm số y=f′(x) (như hình
Lưu về Facebook:
MỤC LỤC
Câu hỏi:
Cho hàm số y=f(x) có đồ thị hàm số y=f′(x) (như hình vẽ). Gọi S là tập tất cả các giá trị nguyên của tham số m thuộc khoảng (-5; 5) sao cho hàm số y=f(x)−mx+2020 có đúng một điểm cực trị. Tổng các phần tử của S bằng

Đáp án án đúng là: B
Lời giải chi tiết:
Chọn B
Ta có y′=f′(x)−m; y′=0 ⇔f′(x)−m=0 ⇔f′(x)=m (1)
Hàm số có đúng một điểm cực trị khi phương trình (1) có nghiệm duy nhất hoặc có hai nghiệm trong đó có 1 nghiệm kép ⇒[m≤−1m≥3
Vì m∈(−5;5) ⇒m∈(−5;−1]∪[3;5).
Mặt khác m nguyên nên m∈{−4;−3;−2;−1;3;4} ⇒S={−4;−3;−2;−1;3;4}
Tổng các phần tử của S bằng: −4−3−2−1+3+4=−3.
Xem thêm các bài tiếp theo bên dưới