Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình chữ nhật vớ

Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình chữ nhật với $\Large AD=2AB=2a$. Cạnh bên $\Large SA=2a$ và vuông góc với đáy. Gọi $\Large M, N$ lần lượt là trung điểm của $\Large SB$ và $\Large SD$. Tính khoảng cách $\Large d$ từ điểm $\Large S$ đến mặt phẳng $\Large (AMN)$.

• A.

  $\Large d=2a$.

• B.

  $\Large d=\dfrac{3a}{2}$.

• C.

  $\Large d=\dfrac{a\sqrt{6}}{3}$.

• D.

  $\Large d=a\sqrt{5}$.

Chọn C

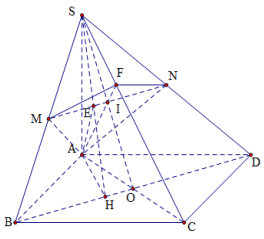
Từ $\Large A$ kẻ đường thẳng vuông góc với $\Large BD$ tại $\Large H$, ta có:

$\Large \left\{\begin{align} & BD\perp (SAH) \\ & MN// BD \end{align}\right.$ $\Large \Rightarrow MN\perp (SAH)\Rightarrow (AMN)\perp (SAH)$

Mặt khác $\Large (AMN)\cap (SAH)=AE$, suy ra: $\Large d\big(S, (AMN)\big)=d(S, AE)$

Xét tam giác vuông $\Large SAH$ có: $\Large AH=\dfrac{AB.AD}{BD}$ $\Large =\dfrac{a.2a}{\sqrt{a^2+4a^2}}=\dfrac{2a\sqrt{5}}{5}$.

$\Large SH=\sqrt{SA^2+AH^2}=\sqrt{4a^2+\dfrac{20a^2}{25}}=\dfrac{2a\sqrt{30}}{5}$.

Vì $\Large MN$ là đường trung bình của tam giác $\Large SBD$ nên $\Large E$ là trung điểm của $\Large SH$, suy ra:

$\Large AE=\dfrac{1}{2}SH=\dfrac{a\sqrt{30}}{5}$.

$\Large d(S, AE)=\dfrac{2S_{\Delta SAE}}{AE}$ $\Large =\dfrac{S_{\Delta SAH}}{AE}=\dfrac{AS.AH}{2.AE}$ $\Large =\dfrac{2a.2a\sqrt{5}}{2.5.\dfrac{a\sqrt{30}}{5}}=\dfrac{a\sqrt{6}}{3}$.