Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình vuông cạnh

Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình vuông cạnh $\Large a$, cạnh bên $\Large SA=y$ $\Large (y > 0)$ và vuông góc với mặt đáy $\Large (ABCD)$. Trên cạnh $\Large AD$ lấy điểm $\Large M$ và đặt $\Large AM=x$ $\Large (0 < x < a)$. Tính thể tích lớn nhất $\Large V_{max}$ của khối chóp $\Large S.ABCM$, biết $\Large x^2+y^2=a^2$.

• A.

  $\Large \dfrac{a^3\sqrt{3}}{9}$.

• B.

  $\Large \dfrac{a^3\sqrt{3}}{3}$.

• C.

  $\Large \dfrac{a^3\sqrt{3}}{8}$.

• D.

  $\Large \dfrac{a^3\sqrt{3}}{5}$.

Chọn C

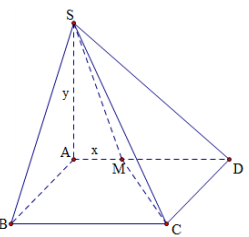
Ta có: $\Large S_{ABCM}=\dfrac{1}{2}(AM+BC).AB=\dfrac{1}{2}(x+a).a$

Vậy thể tích khối chóp $\Large S.ABCM$ là $\Large V=\dfrac{1}{3}SA.S_{ABCM}=\dfrac{1}{3}y.\dfrac{1}{2}(ax+a^2)=\dfrac{a}{6}(xy+ay)$

$\Large \Leftrightarrow V^2=\dfrac{a^2}{36}y^2(x+a)^2$ $\Large \Leftrightarrow \dfrac{36}{a^2}V^2=(a^2-x^2)(x+a)^2$

Xét hàm số $\Large f(x)=(a^2-x^2)(x+a)^2$ trên khoảng $\Large (0; a)$.

Ta có: $\Large f'(x)=-2x(x+a)^2+2(a^2-x^2)(x+a)$ $\Large =2(x+a)^2(a-2x)$

$\Large f'(x)=0$ $\Large \Leftrightarrow x=\dfrac{a}{2}$ (Vì $\Large x > 0$)

Bảng biến thiên

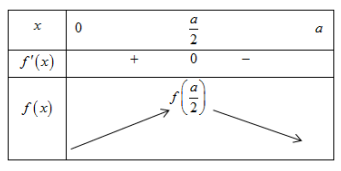
Từ bảng biến thiên suy ra: $\Large \underset{(0; a)}{max}f(x)=f\left(\dfrac{a}{2}\right)$ $\Large =\left(a^2-\dfrac{a^2}{4}\right)\left(\dfrac{a}{2}+a\right)^2=\dfrac{27a^4}{16}$

Vậy $\Large V_{max}=\sqrt{\dfrac{a^2}{36}.\underset{(0; a)}{max}f(x)}$ $\Large =\sqrt{\dfrac{a^2}{36}.\dfrac{27a^4}{16}}=\dfrac{a^3\sqrt{3}}{8}$.