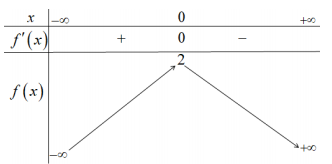
Cho hàm số $\Large y=f(x)$ có đạo hàm trên tập số thực và có bảng biến

Cho hàm số $\Large y=f(x)$ có đạo hàm trên tập số thực và có bảng biến thiên như hình
vẽ bên.

Số nghiệm phân biệt của phương trình $\Large f\left(x-\dfrac{1}{\mathrm{ln}x}\right)=1$ là

 

• A. 2.
• B. 1.
• C. 3.
• D. 4.

+ Từ bảng biến thiên hàm số $\Large y=f(x)$ ta có: $\Large f\left(x-\dfrac{1}{\mathrm{ln}x}\right)=1$ $\Large \Leftrightarrow \left[\begin{align} & x-\dfrac{1}{\mathrm{ln}x}=x_1 < 0 \\ & x-\dfrac{1}{\mathrm{ln}x}=x_2 > 0 \end{align}\right.$

+ Xét hàm số $\Large y=x-\dfrac{1}{\mathrm{ln}x}$.

* Tập xác định: $\Large D=(0; +\infty)\setminus \begin{Bmatrix} 1 \end{Bmatrix}$.

* $\Large {y}'=1+\dfrac{1}{x\mathrm{ln}^2x}$, $\Large {y}' > 0$, $\Large \forall x\in D$.

* Giới hạn: $\Large \underset{x\rightarrow 0^+}{\lim}y=0$; $\Large \underset{x\rightarrow 1^+}{\lim}y=-\infty$; $\Large \underset{x\rightarrow +\infty}{\lim}y=+\infty$.

* Bảng biến thiên:

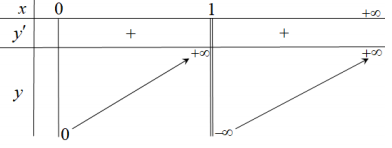
+ Từ bảng biến thiên của hàm số $\Large y=x-\dfrac{1}{\mathrm{ln}x}$ ta có:

* Phương trình $\Large x-\dfrac{1}{\mathrm{ln}x}=x_1$ (1) với $\Large x_1 < 0$ có duy nhất 1 nghiệm.

* Phương trình $\Large x-\dfrac{1}{\mathrm{ln}x}=x_2$ (2) với $\Large x_2 > 0$ có 2 nghiệm phân biệt.

* Các nghiệm của phương trình (1) không trùng với các nghiệm của phương trình (2)
Vậy phương trình đã cho có 3 nghiệm phân biệt.