Cho hàm số $\Large y=f(x)$ có đạo hàm trên $\Large \mathbb{R}$ và có đ

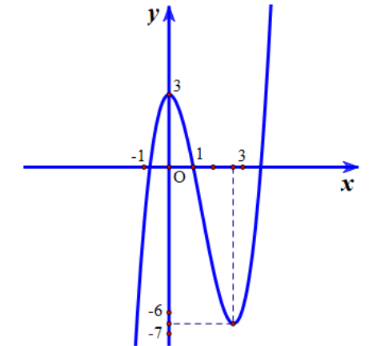
Cho hàm số $\Large y=f(x)$ có đạo hàm trên $\Large \mathbb{R}$ và có đồ thị là đường cong trong hình vẽ bên dưới. Đặt $\Large g(x)=f\big[f(x)\big].$ Tìm số nghiệm của phương trình $\Large {g}'(x)=0.$

 

• A.

  A. $\Large 8.$

• B.

  B. $\Large 2.$

• C.

  C. $\Large 4.$

• D.

  D. $\Large 6.$

Chọn A

Ta có $\Large {g}'(x)={f}'(x).{f}'\big[f(x)\big]=0$ $\Large \Leftrightarrow \left[\begin{align} & {f}'(x)=0 \\ & {f}'\big[f(x)\big]=0 \end{align}\right.$ $\Large \Leftrightarrow \left[\begin{align} & {f}'(x)=0 \\ & f(x)=0 \\ & f(x)=m \in (1; 3) \end{align}\right..$

Phương trình $\Large {f}'(x)=0$ có $\Large 2$ nghiệm

Phương trình $\Large f(x)=0$ có $\Large 3$ nghiệm

Phương trình $\Large f(x)=m \in (1; 3)$ có $\Large 3$ nghiệm

Vậy phương trình có $\Large 8$ nghiệm.