Cho hàm số $\Large y=f(x)=\dfrac{ax+b}{cx+d}$ (với $\Large a, b, c, d

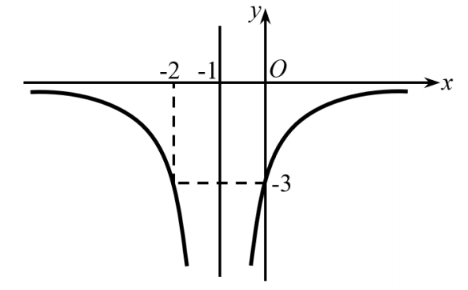
Cho hàm số $\Large y=f(x)=\dfrac{ax+b}{cx+d}$ (với $\Large a, b, c, d \in \mathbb{R}, c \neq 0, d \neq 0$) có đồ thị là $\Large (C).$ Biết đồ thị của hàm số $\Large y={f}'(x)$ như hình vẽ dưới

Biết đồ thị $\Large (C)$ cắt trục tung tại điểm có tung độ bằng $\Large 2.$ Tiếp tuyến của $\Large (C)$ tại giao điểm của $\Large (C)$ với trục hoành có phương trình là

• A.

  A. $\Large x-3y-2=0.$

• B.

  B. $\Large x-3y+2=0.$

• C.

  C. $\Large x+3y-2=0.$

• D.

  D. $\Large x+3y+2=0.$

Chọn C

Ta có $\Large {y}'={f}'(x)=\dfrac{ad-bc}{\big(cx+d\big)^2}.$

Đồ thị $\Large (C)$ cắt trục tung tại điểm có tung độ bằng $\Large 2$ nên $\Large f(0)=2 \Rightarrow \dfrac{b}{d}=2.$

Từ đồ thị của hàm số $\Large y={f}'(x)$ ta có: 

+ Đồ thị hàm số $\Large y={f}'(x)$ có tiệm cận đứng là đường thẳng $\Large x=-1$ nên $\Large -\dfrac{d}{c}=-1 \Leftrightarrow \dfrac{d}{c}=1.$

+ Đồ thị hàm số $\Large y={f}'(x)$ đi qua điểm $\Large (-2; -3)$ nên $\Large {f}'(-2) =-3 \Rightarrow -3=\dfrac{ad-bc}{(-2c+d)^2}.$

+ Đồ thị hàm số $\Large y={f}'(x)$ cắt trục tung tại điểm $\Large (0; -3)$ nên $\Large {f}'(0)=-3 \Rightarrow -3 =\dfrac{ad-bc}{d^2}.$

Ta có hệ phương trình $\Large \left\{\begin{align} & b=2d=2c \\ & \dfrac{ad-bc}{(d-2c)^2}=-3 \\ & \dfrac{ad-bc}{d^2}=-3 \end{align}\right.$ $\Large \Leftrightarrow \left\{\begin{align} & b=2c=2d=2t (t \neq 0) \\ & \dfrac{at-2t.t}{(t-2t)^2}=-3 \\ & \dfrac{at-2t.t}{t^2}=-3 \end{align}\right.$ $\Large \left\{\begin{align} & b=2c=2d=2t \\ & at-2t^2=-3t^2 \end{align}\right.$ $\Large \Leftrightarrow \left\{\begin{align} & b=2c=2d=2t \\ & a=-t \end{align}\right..$

Suy ra $\Large y=f(x)=\dfrac{-tx+2t}{tx+t}=\dfrac{-x+2}{x+1}$ và $\Large {y}'={f}'(x)=\dfrac{-3}{(x+1)^2}.$

Giao điểm của đồ thị $\Large (C)$ với trục hoành là $\Large A(2; 0)$

$\Large \Rightarrow$ Hệ số góc của tiếp tuyến tại điểm $\Large A$ là $\Large k={f}'(2)=\dfrac{-3}{(2+1)^2}=-\dfrac{1}{3}.$

Vậy phương trình tiếp tuyến là $\Large y=-\dfrac{1}{3}(x-2)+0 \Leftrightarrow x+3y-2=0.$