Xét các số thực dương $\Large x, y$ thỏa mãn $\Large \mathrm{log}_{\df

Xét các số thực dương $\Large x, y$ thỏa mãn $\Large \mathrm{log}_{\dfrac{1}{2}}x+\mathrm{log}_{\dfrac{1}{2}}y \leq \mathrm{log}_{\dfrac{1}{2}}(x+y^2).$ Tìm giá trị nhỏ nhất $\Large P_{\min}$ của biểu thức $\Large P=x+3y.$

• A.

  A. $\Large P_{\min}=\dfrac{17}{2}.$

• B.

  B. $\Large P_{\min}=8.$

• C.

  C. $\Large P_{\min}=9.$

• D.

  D. $\Large P_{\min}=\dfrac{25\sqrt{2}}{4}.$

Chọn C

Ta có $\Large \mathrm{log}_{\dfrac{1}{2}}x+\mathrm{log}_{\dfrac{1}{2}}y \leq \mathrm{log}_{\dfrac{1}{2}}(x+y^2)$ $\Large \Leftrightarrow \mathrm{log}_{\dfrac{1}{2}}(xy) \leq \mathrm{log}_{\dfrac{1}{2}}(x+y^2)$ $\Large \Leftrightarrow xy \geq x+y^2$ $\Large \Leftrightarrow (y-1)x \geq y^2.$

Do $\Large y > 0 \Rightarrow y^2 > 0 \Rightarrow (y-1)x \geq y^2 > 0.$

Mà $\Large x > 0$ nên $\Large y-1 > 0 \Leftrightarrow y > 1.$

Khi đó ta có $\Large x \geq \dfrac{y^2}{y-1}.$ Suy ra $\Large P=x+3y \geq \dfrac{y^2}{y-1}+3y$

Xét hàm số $\Large f(y)=\dfrac{y^2}{y-1}+3y$ trên $\Large (1; +\infty).$

Ta có $\Large {f}'(y)=\dfrac{y^2-2y}{(y-1)^2}+3=\dfrac{4y^2-8y+3}{(y-1)^2}$

$\Large {f}'(y)=0$ $\Large \Leftrightarrow \left[\begin{align} & y=\dfrac{1}{2} \notin (1; +\infty) \\ & y=\dfrac{3}{2} \in (1; +\infty) \end{align}\right.$

Bảng biến thiên: 

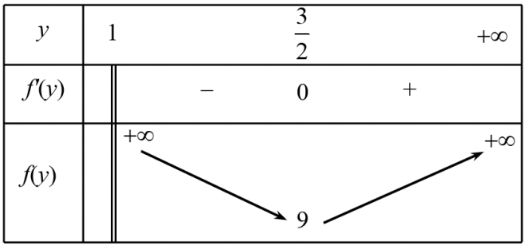
Từ bảng biến thiên suy ra $\Large f(y) \geq f\bigg(\dfrac{3}{2}\bigg)=9.$

Vậy $\Large P \geq f(y) \geq 9.$

Dấu "$\Large =$" xảy ra khi và chỉ khi $\Large \left\{\begin{align} & y=\dfrac{3}{2} \\ & x=\dfrac{y^2}{y-1}=\dfrac{9}{2} \end{align}\right..$