Cho hàm số $\large y=f(x)$ có bảng biến thiên như sau: Số nghiệm thực

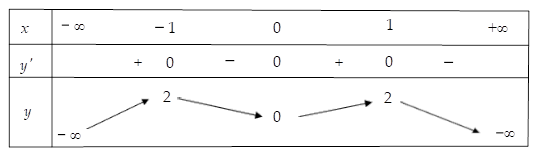
Cho hàm số $\large y=f(x)$ có bảng biến thiên như sau:

Số nghiệm thực thuộc đoạn $\large \left[ 0; 2\pi\right]$ của phương trình $\large 3f(\sin 2x)-4=0$ là: 

• A. 8
• B. 2
• C. 4
• D. 6

Chọn A

Ta có: $\large 3f(\sin 2x)-4=0\Leftrightarrow f(\sin 2x)=\dfrac{4}{3}\Leftrightarrow $ $\large \left[\begin{align}& \sin 2x=a( a<-1)\\& \sin 2x=b, (-11)\\\end{align}\right.$

Vẽ đồ thị hàm số $\large y=\sin 2x$ trên đoạn $\large \left[0; 2\pi]\right]$

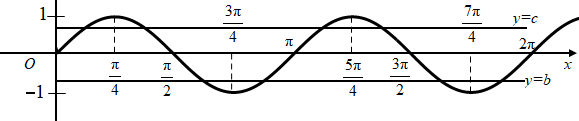
Dựa vào đồ thị hàm số $\large y=\sin 2x$ trên đoạn $\large \left[0; 2\pi \right]$ ta thấy 

+ Phương trình $\large \sin 2x=a, (a<-1)$ vô nghiệm 

+ Phương trình $\large \sin 2x=b, (-1

+ Phương trình $\large \sin 2x = c, (0

+ Phương trình $\large \sin 2x=d, (d>1)$ vô nghiệm

Vậy PT đã cho có tất cả 8 nghiệm