Cho hàm số $\Large y=f(x)$ biết hàm số $\Large f(x)$ có đạo hàm $\Larg

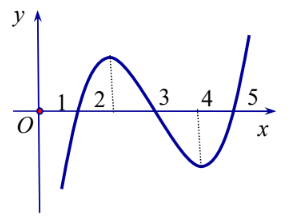
Cho hàm số $\Large y=f(x)$ biết hàm số $\Large f(x)$ có đạo hàm $\Large {f}'(x)$ và hàm số $\Large y={f}'(x)$ có đồ thị như hình vẽ. Đặt $\Large g(x)=f(x+1).$ Kết luận nào sau đây đúng?

• A.

  A. Hàm số $\Large g(x)$ đồng biến trên khoảng $\Large (3; 4).$

• B.

  B. Hàm số $\Large g(x)$ đồng biến trên khoảng $\Large (0; 1).$

• C.

  C. Hàm số $\Large g(x)$ nghịch biến trên khoảng $\Large (2; +\infty).$

• D.

  D. Hàm số $\Large g(x)$ nghịch biến trên khoảng $\Large (4; 6).$

Chọn B

$\Large g(x)=f(x+1).$

Ta có: $\Large {g}'(x)={f}'(x+1)$

Hàm số $\Large g(x)$ đồng biến $\Large \Leftrightarrow {g}'(x) > 0$ $\Large \Leftrightarrow {f}'(x+1) > 0$ $\Large \Leftrightarrow \left[\begin{align} & x+1 > 5 \\ & 1 < x+1 < 3 \end{align}\right.$ $\Large \Leftrightarrow \left[\begin{align} & x > 4 \\ & 0 < x < 2 \end{align}\right..$

Hàm số $\Large g(x)$ nghịch biến $\Large \Leftrightarrow {g}'(x) < 0$ $\Large \Leftrightarrow {f}'(x+1) < 0$ $\Large \Leftrightarrow \left[\begin{align} & 3 < x+1 < 5 \\ & x+1 < 1 \end{align}\right.$ $\Large \Leftrightarrow \left[\begin{align} & 2 < x < 4 \\ & x < 0 \end{align}\right..$ 

Vậy hàm số $\Large g(x)$ đồng biến trên khoảng $\Large (0; 2); (4; +\infty)$ và nghịch biến trên khoảng $\Large (2; 4); (-\infty; 0).$