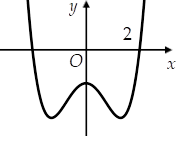
Cho hàm số $\large y=ax^4+bx^2+c$ có đồ thị như hình bên. Mệnh đề nào

Cho hàm số $\large y=ax^4+bx^2+c$ có đồ thị như hình bên. Mệnh đề nào sau đây sai ?

• A. a + b + c <0
• B. b > 0
• C. c < 0
• D. a > 0

Ta có:
Dựa vào đồ thị của hàm số ta có a > 0 và đồ thị hàm số cắt Oy tại điểm có tung độ âm $\large c<0$

$\large y=ax^4+bx^2+c\Rightarrow y'=4ax^3+2bx$

Xét $\large y'=0\Leftrightarrow x(4ax^2+2b)=0$

Dựa vào đồ thị của hàm số ta có hàm số có 3 điểm cực trị $\large \Rightarrow ab<0\Rightarrow b<0$

Vậy B sai.