Cho hàm số $\large y=f(x)$ có đạo hàm trên $\large \mathbb{R}$ là $\la

Cho hàm số $\large y=f(x)$ có đạo hàm trên $\large \mathbb{R}$ là $\large f'(x)=(x^2-3x)(x^3-4x)$. Điểm cực đại của hàm số đã cho là: 

• A. x = 0
• B. x = 3
• C. x = -2
• D. x = 2

Ta có: $\large f'(x)=0\Leftrightarrow (x^2-3x)(x^3-4x)=0$ $\large \Leftrightarrow \left[\begin{align}& x=\pm 2\\& x=0 \text{ bội hai }\\& x=3\\\end{align}\right.$

Bảng xét dấu của $\large f'(x)$

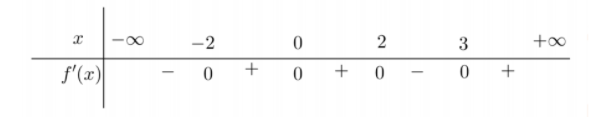
Ta thấy $\large f'(x)$ đổi dấu từ + sang - khi đi qua điểm x = 2. Vậy điểm cực đại của hàm số đã cho là $\large x=2$