Cho hàm số $\large y = x^{3} - 3x^{2} + m -1$. Tổng tất cả các giá trị

Cho hàm số $\large y = x^{3} - 3x^{2} + m -1$. Tổng tất cả các giá trị nguyên của tham số m để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt bằng

• A.

  -9

• B.

  9

• C.

  15

• D.

  -15

Phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành là:
    $\large x^{3} - 3x^{2} + m -1=0 \Leftrightarrow x^{3} - 3x^{2} - 1 = -m$ (*)
Xét hàm số $\large f(x) = x^{3} - 3x^{2} - 1$
Ta có: $\large f'(x) = 3x^{2} - 6x = 3x(x - 2)$
Khi đó: $\large f'(x) = 0 \Leftrightarrow 3x(x - 2) = 0 \Leftrightarrow \left[\begin{align} &x = 0 \\ &x = 2 \end{align}\right.$
Bảng biến thiên 

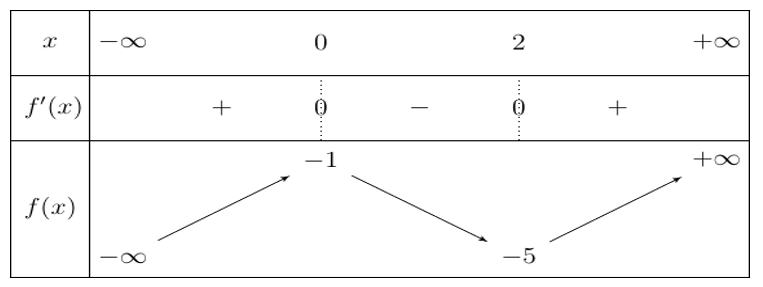
Đồ thị hàm số cắt trục hoành tại ba điểm phân biệt $\large \Leftrightarrow$ (*) có 3 nghiệm phân biệt
$\large  \Leftrightarrow -5 < -m < -1 \Leftrightarrow 1 < m < 5$
Do đó $\large m \in \mathbb{R} \Rightarrow m \in {{2;3;4}}$
Vậy tổng các giá trị nguyên của tham số m là 9