Cho hàm số $\Large y = f(x)$ liên tục trên $\Large \mathbb{R}$ và có đ

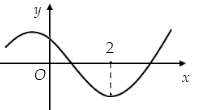
Cho hàm số $\Large y = f(x)$ liên tục trên $\Large \mathbb{R}$ và có đồ thị như hình vẽ bên.

Tìm m để bất phương trình $\large f(x)\geq \dfrac{x+1}{x+2}+m$ nghiệm đúng với mọi $\large x\in [0; 1].$

• A.

  $\large m\leq f(1)-\dfrac{2}{3}$

• B.

  $\large m\geq f(0)-\dfrac{1}{2}$

   
• C.

  $\large m< f(1)-\dfrac{2}{3}$

• D.

  $\large m> f(0)-\dfrac{1}{2}$

Từ đồ thị hàm số ta thấy trên đoạn $\large [0; 1]$ hàm số nghịch biến nên $\large f'(x)\leq 0, \forall x\in [0; 1]$

Xét hàm số $\large g(x)=f(x)-\dfrac{x+1}{x+2}$. Ta có $\large g'(x)=f'(x)-\dfrac{1}{(x+2)^2}<0,\forall x\in [0; 1]$

Do đó giá trị nhỏ nhất của hàm số g(x) là: $\large \underset{[0;1]}{\min} g(x)=g(1)=f(1)-\dfrac{2}{3}$

$\large f(x)\geq \dfrac{x+1}{x+2}+m$ nghiệm đúng với mọi $\large x\in [0; 1]$ khi và chỉ khi:

$\large \underset{[0; 1]}{\min} g(x)\geq m\Rightarrow m\leq f(1)-\dfrac{2}{3}$