Cho hàm số $\Large f(x)$. Hàm số $\Large y={f}'(x)$ có đồ thị như hình

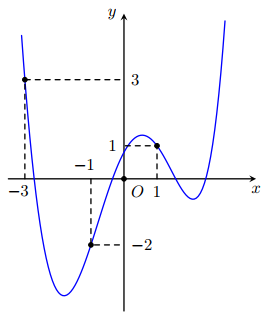
Cho hàm số $\Large f(x)$. Hàm số $\Large y={f}'(x)$ có đồ thị như hình sau.

Tìm tất cả các giá trị thực của tham số $\Large m$ để bất phương trình $\Large 2f(\sin x -2)-\dfrac{2\sin ^3x}{3}+\sin x > m+\dfrac{5\cos 2x}{4}$ nghiệm đúng với mọi $\Large x\in \left(-\dfrac{\pi}{2}; \dfrac{\pi}{2}\right)$

• A.

  $\Large m < 2f(-1)+\dfrac{19}{12}$.

• B.

  $\Large m\leq 2f(-1)+\dfrac{19}{12}$.

• C.

  $\Large m\leq 2f(-3)+\dfrac{11}{12}$.

• D.

  $\Large m < 2f(-3)+\dfrac{11}{12}$.

Chọn B
Ta có $\Large 2f(\sin x-2)-\dfrac{2\sin ^3x}{3}+\sin x > m+\dfrac{5\cos 2x}{4}$.

$\Large \Leftrightarrow m < 2f(\sin x-2)-\dfrac{2\sin ^3x}{3}+\sin x-\dfrac{5\cos 2x}{4}$.

$\Large \Leftrightarrow m < 2f(\sin x-2)-\dfrac{2\sin ^3x}{3}+\sin x-\dfrac{5(1-2\sin ^2x)}{4}$ (1).

Đặt $\Large t= \sin x-2$. Do $\Large x\in \left(-\dfrac{\pi}{2}; \dfrac{\pi}{2}\right)$$\Large \Rightarrow -1 < \sin x < 1$$\Large \Rightarrow -3 < t < -1$.

Khi đó (1) trở thành $\Large m < 2f(t)-\dfrac{2(t+2)^3}{3}+t-\dfrac{5\left(1-2(t+2)^2\right)}{4}$.

Gọi $\Large g(t)=2f(t)-\dfrac{2(t+2)^3}{3}+t-\dfrac{5\left(1-2(t+2)^2\right)}{4}$.

Ta có $\Large {g}'(t)=2{f}'(t)-2(t+2)^2+1+5(t+2)$.

$\Large {g}'(t)=0\Leftrightarrow 2{f}'(t)-2(t+2)^2+1+5(t+2)=0$$\Large \Leftrightarrow {f}'(t)=t^2+\dfrac{3}{2}t-\dfrac{3}{2}$.

Vẽ đồ thị Parabol $\Large (P): y=x^2+\dfrac{3}{2}x-\dfrac{3}{2}$ trên cùng hệ trục $\Large Oxy$ với đồ thị $\Large y={f}'(x)$ như hình vẽ sau (đường màu đỏ nét đứt).

Parabol $\Large (P)$ có đỉnh $\Large I\left(-\dfrac{3}{4}; -\dfrac{33}{16}\right)$ và đi qua điểm $\Large (-3; 3); (-1; -2); (1; 1)$.

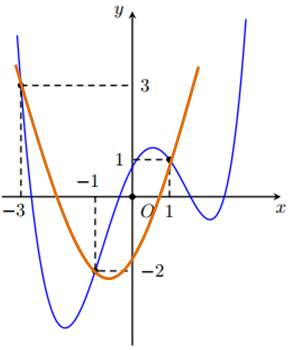
Dựa vào đồ thị ta thấy $\Large {f}'(t) < t^2+\dfrac{3}{2}t-\dfrac{3}{2}t$, $\Large \forall t\in (-3; -1)$ hay $\Large {g}'(t) < 0$, $\Large \forall t\in (-3; -1)$.

Vậy $\Large m < g(t)$, $\Large \forall t\in (-3; -1)\Leftrightarrow m \leq g(-1)$$\Large \Leftrightarrow m\leq 2f(-1)+\dfrac{19}{12}$.