Cho $\Large x$; $\Large y$ là hai số thực dương thỏa mãn $\Large x\neq

Cho $\Large x$; $\Large y$ là hai số thực dương thỏa mãn $\Large x\neq y$ và $\Large \left(2^x+\dfrac{1}{2^x}\right)^y < \left(2^y+\dfrac{1}{2^y}\right)^x$. Tìm giá trị nhỏ nhất của biểu thức $\Large P=\dfrac{x^2+3y^2}{xy-y^2}$.

• A.

  $\Large min\ P=\dfrac{9}{2}$.

• B.

  $\Large min\ P=\dfrac{13}{2}$.

• C.

  $\Large min\ P=6$.

• D.

  $\Large min\ P=-2$.

Chọn C

Ta có: $\Large \left(2^x+\dfrac{1}{2^x}\right)^y < \left(2^y+\dfrac{1}{2^y}\right)^x$

$\Large \Leftrightarrow \left(\dfrac{4^x+1}{2^x}\right)^y$ < $\Large \left(\dfrac{4^y+1}{2^y}\right)^x$ $\Large \Leftrightarrow \dfrac{(4^x+1)^y}{2^{xy}}$ < $\Large \dfrac{(4^y+1)^x}{2^{xy}}$ $\Large \Leftrightarrow (4^x+1)^y < (4^y+1)^x$

$\Large \Leftrightarrow y\mathrm{ln}(4^x+1) < x\mathrm{ln}(4^y+1)$$\Large \Leftrightarrow \dfrac{\mathrm{ln}(4^x+1)}{x} < \dfrac{\mathrm{ln}(4^y+1)}{y}$ (*).

Xét hàm đặc trưng $\Large f(t)=\dfrac{\mathrm{ln}(4^t+1)}{t}$ với $\Large t > 0$.

Ta có:

$\Large {f}'(t)=\dfrac{\left[\mathrm{ln}(4^t+1)\right]'.t-\mathrm{ln}(4^t+1).t'}{t^2}$=$\Large \dfrac{\dfrac{4^t.\mathrm{ln}4}{4^t+1}-\mathrm{ln}(4^t+1)}{t^2}$=$\Large \dfrac{4^t.\mathrm{ln}4^t-(4^t+1)\mathrm{ln}(4^t+1)}{t^2.(4^t+1)} < 0$, $\Large \forall t > 0$.

$\Large \Rightarrow$ Hàm $\Large f(t)$ là hàm nghịch biến trên khoảng $\Large (0; +\infty)$.

Do đó bất phương trình (*) $\Large \Leftrightarrow f(x) < f(y)$ $\Large \Leftrightarrow x > y > 0 \Rightarrow \dfrac{x}{y} > 1$.

Khi đó: $\Large P=\dfrac{x^2+3y^2}{xy-y^2}$=$\Large \dfrac{\left(\dfrac{x}{y}\right)^2+3}{\dfrac{x}{y}-1}$ (Do $\Large y > 0$),

Đặt $\Large t=\dfrac{x}{y} > 1$ thì biểu thức trở thành: $\Large P=\dfrac{t^2+3}{t-1}$ với $\Large t > 1$.

Ta có: $\Large {P}'=\dfrac{2t(t-1)-(t^2+3)}{(t-1)^2}$=$\Large \dfrac{t^2-2t-3}{(t-1)^2}=0$$\Large \Leftrightarrow t^2-2t-3=0$$\Large \Leftrightarrow \left[\begin{align} & t=-1 \\ & t=3 \end{align}\right.$

Bảng biến thiên:

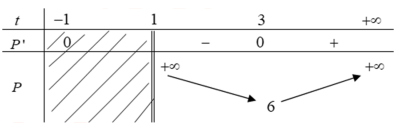
Vậy $\Large P_{min}=6$.