Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình bình hành.

Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình bình hành. Hai điểm $\Large M$, $\Large N$ lần lượt thuộc các đoạn thẳng $\Large AB$ và $\Large AD$ ($\Large M$ và $\Large N$ không trùng với $\Large A$) sao cho $\Large 2\dfrac{AB}{AM}+3\dfrac{AD}{AN}=8$. Kí hiệu $\Large V$, $\Large V_1$ lần lượt là thể tích của các khối chóp $\Large S.ABCD$ và $\Large S.MBCDN$. Tìm giá trị lớn nhất của tỉ số $\Large \dfrac{V_1}{V}$.

• A.

  $\Large \dfrac{13}{16}$.

• B.

  $\Large \dfrac{11}{12}$.

• C.

  $\Large \dfrac{1}{6}$.

• D.

  $\Large \dfrac{2}{3}$.

Chọn A

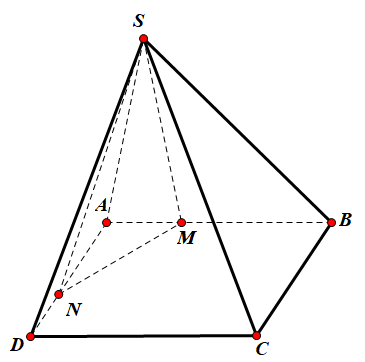
Đặt $\Large \dfrac{AB}{AM}=x$; $\Large \dfrac{AD}{AN}=y$, $\Large x, y\geq 1$.

Ta có $\Large \dfrac{V_{S.AMN}}{V_{S.ABCD}}=\dfrac{S_{AMN}}{S_{ABCD}}$=$\Large \dfrac{\dfrac{1}{2}AM.AN.sin\widehat{DAB}}{AB.AD.sin\widehat{DAB}}$=$\Large \dfrac{1}{2}.\dfrac{AM}{AB}.\dfrac{AN}{AD}=\dfrac{1}{2yx}$.

Theo bài ra $\Large \dfrac{V_{S.AMN}}{V_{S.ABCD}}=\dfrac{1}{2y\left(4-\dfrac{3}{2}y\right)}$; $\Large 1\leq y\leq 2$ (do $\Large x\geq 1$).

Ta có $\Large \dfrac{V_1}{V}=1-\dfrac{V_{S.AMN}}{V_{S.ABCD}}=1-\dfrac{1}{y(8-3y)}$; $\Large 1\leq y\leq 2$.

Áp dụng BĐT Côsi ta có $\Large 3y(8-3y)\leq \left(\dfrac{3y+8-3y}{2}\right)^2=16$

Suy ra $\Large \dfrac{V_1}{V}\leq 1-\dfrac{3}{16}=\dfrac{13}{16}$ $\Large \Rightarrow max\dfrac{V_1}{V}=\dfrac{13}{16}$. Dấu bằng xảy ra khi $\Large y=\dfrac{4}{3}$, $\Large x=2$.