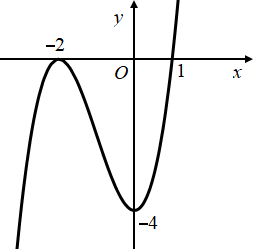
Cho hàm số $\Large y=f(x)=ax^3+bx^2+cx+d$ có đồ thị như hình dưới đây

Cho hàm số $\Large y=f(x)=ax^3+bx^2+cx+d$ có đồ thị như hình dưới đây

Có tất cả bao nhiêu giá trị nguyên của tham số $\Large m\in (-5; 5)$ để phương trình $\Large f^2(x)-(m+4)|f(x)|+2m+4=0$ có 6 nghiệm phân biệt.

• A. 4.
• B. 2.
• C. 5.
• D. 3.

Chọn D
Ta có phương trình $\Large f^2(x)-(m+4)|f(x)|+2m+4=0$

$\Large \Leftrightarrow \left(|f(x)|-2\right)\left(|f(x)|-m-2\right)=0$$\Large \Leftrightarrow \left[\begin{align} & |f(x)|=2\ (1) \\ & |f(x)|=m+2\ (2) \end{align}\right.$.

Từ đồ thị hàm số $\Large y=f(x)$ ta có đồ thị hàm số $\Large y=|f(x)|$ như sau:

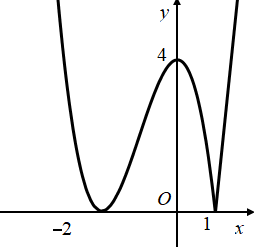
Từ đồ thị trên, ta có phương trình (1) có 4 nghiệm phân biệt.
Để phương trình đã cho có 6 nghiệm phân biệt thì phương trình (2) có 2 nghiệm phân biệt và khác các nghiệm của (1).

Suy ra $\Large \left[\begin{align} & m+2 > 4 \\ & m+2=0 \end{align}\right.$ $\Large \Leftrightarrow \left[\begin{align} & m > 2 \\ & m=-2 \end{align}\right.$.

Vì $\Large m$ nguyên và $\Large m\in (-5; 5)\Rightarrow m\in \begin{Bmatrix} -2; 3; 4 \end{Bmatrix}$.