Cho hàm số đa thức $\Large f(x)$ có đạo hàm trên $\Large \mathbb{R}$.

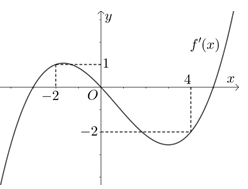
Cho hàm số đa thức $\Large f(x)$ có đạo hàm trên $\Large \mathbb{R}$. Biết $\Large f(0)=0$ và đồ thị hàm số $\Large y={f}'(x)$ như hình sau:

Hàm số $\Large g(x)=|4f(x)+x^2|$ đồng biến trên khoảng nào dưới đây?

• A.

  $\Large (0; 4)$.

• B.

  $\Large (4; +\infty)$.

• C.

  $\Large (-\infty; -2)$.

• D.

  $\Large (-2; 0)$.

Chọn A

+ Xét hàm số $\Large h(x)=4f(x)+x^2\Rightarrow {h}'(x)=4{f}'(x)+2x=0$$\Large \Leftrightarrow {f}'(x)=-\dfrac{1}{2}x$.

+ Bằng cách vẽ đồ thị ta thu được các nghiệm của phương trình trên là $\Large x=-2$; $\Large x=0$; $\Large x=4$

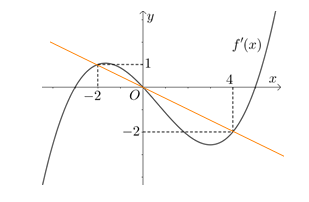
Vì $\Large f(0)=0\Rightarrow h(0)=0$.

Ta có bảng sau trong đó $\Large x_1$, $\Large x_2$ là 2 nghiệm của $\Large h(x)=0$.

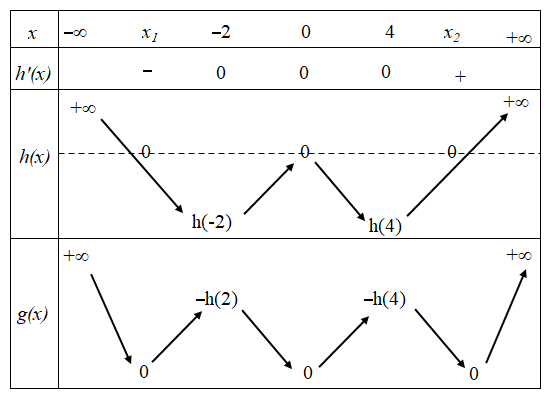
Từ bảng xét dấu ta thu được $\Large g$ đồng biến trên (0; 4).