Cho hàm số f(x) xác định và liên tục trên $\Large \mathbb R \backslash

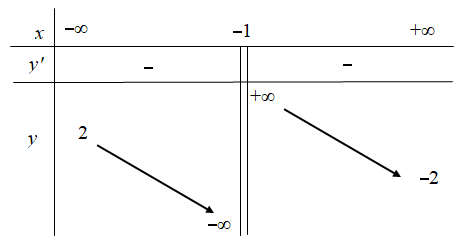
Cho hàm số f(x) xác định và liên tục trên $\Large \mathbb R \backslash\{-1\}$ có bảng biến thiên như sau

Hỏi đồ thị hàm số $\Large y=\dfrac{1}{f(x)}$ có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?

• A. 4
• B. 3
• C. 2
• D. 1

Chọn A

Ta có: $\Large \lim _{x \rightarrow-\infty} f(x)=2 \Rightarrow \lim _{x \rightarrow-\infty} \dfrac{1}{f(x)}=\dfrac{1}{2}$; $\Large \lim _{x \rightarrow+\infty} f(x)=-2 \Rightarrow \lim _{x \rightarrow+\infty} \dfrac{1}{f(x)}=-\dfrac{1}{2}$

Suy ra đồ thị hàm số $\Large y=\dfrac{1}{f(x)}$ có hai đường tiệm cận ngang là $\Large y=\dfrac{1}{2}$ và $\Large y=-\dfrac{1}{2}$

Dựa vào bảng biến thiên của hàm số $\Large y=f(x)$ ta thấy: phương trình $\Large y=f(x)$  có hai nghiệm phân biệt $\Large x_{1} < -1 < x_{2}$

Khi đó: $\Large f\left(x_{1}\right)=f\left(x_{2}\right)=0$

Ta có: $\Large \left\{\begin{array}{l} \lim _{x \rightarrow x_{1}^{-}} f(x)=0 \\ f(x) > 0 \text { khi } x \rightarrow x_{1}^{-} \end{array} \Rightarrow \lim _{x \rightarrow x_{1}^{-}} \dfrac{1}{f(x)}=+\infty\right.$ và $\Large \left\{\begin{array}{l} \lim _{x \rightarrow x_{2}^{-}} f(x)=0 \\ f(x) > 0 \text { khi } x \Rightarrow x_{2}^{-} \end{array} \Rightarrow \lim _{x \rightarrow x_{2}^{-}} \dfrac{1}{f(x)}=+\infty\right.$

Vậy đồ thị hàm số $\Large y=\dfrac{1}{f(x)}$ có hai tiệm cận đứng là đường thẳng $\Large x=x_{1} \text { và } x=x_{2}$

Do đó chọn A