Cho hàm số bậc bốn $\Large y=f(x)$ có đồ thị như hình vẽ bên. Có bao n

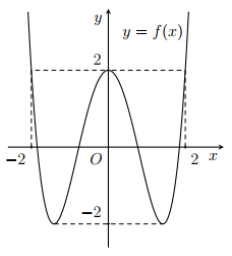
Cho hàm số bậc bốn $\Large y=f(x)$ có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của tham số $\Large m$ thuộc đoạn $\Large [0; 20]$ sao cho giá trị nhỏ nhất của hàm số $\Large g(x)=\left||2f(x)+m+4|-f(x)-3\right|$ trên đoạn $\Large [-2; 2]$ không bé hơn 1?

• A. 18.
• B. 19.
• C. 20.
• D. 21.

Quan sát đồ thị hình vẽ, ta thấy $\Large -2\leq f(x)\leq 2$, $\Large \forall x\in [-2; 2]$ $\Large \Rightarrow 2f(x)+4\geq 0$, $\Large \forall x\in [-2; 2]$.

Vì $\Large m\in [0; 20]$ nên $\Large 2f(x)+m+4\geq 0$, $\Large \forall x\in [-2; 2]$.

Suy ra $\Large \left|2f(x)+m+4\right|=2f(x)+m+4$, $\Large \forall x\in [-2; 2]$.

Khi đó $\Large g(x)=\left|2f(x)+m+4-f(x)-3\right|=\left|f(x)+m+1\right|$, $\Large \forall x\in [-2; 2]$.

Với $\Large m=0$ thì $\Large g(x)=\left|f(x)+1\right|$, $\Large \forall x\in [-2; 2]$. Do $\Large -2\leq f(x)\leq 2$, $\Large \forall x\in [-2; 2]$

$\Large \Rightarrow -1\leq f(x)+1\leq 3$, $\Large \forall x\in [-2; 2]$ $\Large \Rightarrow 0\leq |f(x)+1|\leq 3$, $\Large \forall x\in [-2; 2]$.

$\Large \Rightarrow \underset{[-2; 2]}{\min g(x)}=0$ (không thỏa mãn yêu cầu bài toán) $\Large \Rightarrow m=0$ không là giá trị cần tìm.

Với $\Large m\in [1; 20]$ ta có $\Large m+1\in [2; 21]$ $\Large \Rightarrow 0\leq f(x)+m+1\leq 23$ $\Large \Rightarrow g(x)=f(x)+m+1$.

Từ $\Large -2\leq f(x)\leq 2$, $\Large \forall x\in [-2; 2]$, suy ra $\Large f(x)+m+1\geq m+1-2=m-1$ $\Large \Rightarrow \underset{[-2; 2]}{\min g(x)}=m-1$.

Yêu cầu bài toán $\Large \underset{[-2; 2]}{\min g(x)}\geq 1$ $\Large \Leftrightarrow m-1\geq 1$ $\Large \Leftrightarrow m\geq 2$. Suy ra $\Large m\in [2; 20]$.

Mà $\Large m\in \mathbb{Z}$ nên $\Large m\in \begin{Bmatrix} 2; 3; 4;...; 20 \end{Bmatrix}$.

Vậy có tất cả $\Large 20-2+1=19$ giá trị nguyên của $\Large m$ thỏa mãn yêu cầu bài toán.

Chọn đáp án B