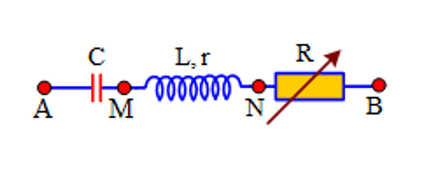
Cho đoạn mạch xoay chiều như hình vẽ. Đặt vào hai đầu A, B điệ

Cho đoạn mạch xoay chiều như hình vẽ. Đặt vào hai đầu A, B điện áp xoay chiều $\Large\ {{u}_{AB}}=100\sqrt{2}\cos \left( 100\pi t-\dfrac{\pi }{2} \right)V$. Biết cuộn dây có $\Large\ L=\dfrac{1}{\pi \sqrt{3}}H, r = 20 \Omega$; tụ điện có $\Large\ C=\dfrac{\sqrt{3}{{.10}^{-4}}}{2\pi }F$; biến trở R. Để ở thời điểm t có $\Large\ {{u}_{AB}}=-100\sqrt{2}V$ và $\Large\ u_{MN} = 0$ V thì R phải bằng 

• A.

   A. $\Large\ \dfrac{440}{3}\Omega$ 

• B.

  B. 200 $\Large\ \Omega$

• C.

  C. $\Large\ 100\sqrt{2}\Omega$

• D.

  D. $\Large\ \dfrac{300}{4}\Omega$ 

+ $\Large\ {{Z}_{L}}=\dfrac{100}{\sqrt{3}}\Omega ;{{Z}_{C}}=\dfrac{200}{\sqrt{3}}\Omega .$ 
+ Khi $\Large\ {{u}_{AB}}=-{{U}_{0}}=-100\sqrt{2}V\Rightarrow {{u}_{MN}}=0\Rightarrow {{u}_{AB}}\bot {{u}_{MN}}$ 
$\Large\ \Rightarrow \dfrac{{{Z}_{L}}}{r}\dfrac{{{Z}_{C}}-{{Z}_{L}}}{R+r}=1\Leftrightarrow \dfrac{\dfrac{100}{\sqrt{3}}}{20}\dfrac{\dfrac{200}{\sqrt{3}}-\dfrac{100}{\sqrt{3}}}{R+20}=1\Rightarrow R=\dfrac{440}{3}\left( \Omega  \right)$ 
→ Đáp án A