Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình

Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhât ABCD có AB và CD thuộc hai đáy của khối trụ. Biết $\large AD= 6$ và góc CAD bằng $\large 60^\circ$. Thể tích của khối trụ là

• A. A. $\large 24\pi$
• B. B. $\large 112\pi$
• C. C. $\large 126\pi$
• D. D. $\large 162\pi$

Chọn D

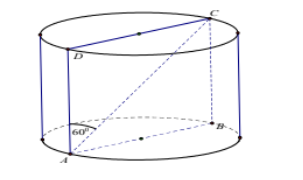
Xét tam giác vuông DAC, có $\large CD= AD.\tan 60^\circ= 6\sqrt{3}$

Suy ra: bán kính đường tròn đáy của khối trụ là: $\large R = \dfrac{CD}{2} = 3\sqrt{3}$

Chiều cao của khối trụ là $\large h = AD= 6$

Vậy thể tích của khối trụ là $\large V= \pi. R^2.h = \pi .(3\sqrt{3})^2.6 = 162\pi$