Xét các số thực thỏa mãn a>b>1. Tìm giá trị nhỏ nhất $\larg
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Xét các số thực thỏa mãn a>b>1. Tìm giá trị nhỏ nhất Pmin của biểu thức P=log2ab(a2)+3logb(ab)
Đáp án án đúng là: C
Lời giải chi tiết:
Chọn C
P=log2ab(a2)+3logb(ab)=(112.loga(ab))2+3logb(a−1)=4(1−logab)2+3logab−3
Đặt t=logab(0<t<1)
Ta được biểu thức: P=f(t)=4(1−t)2+3t−3;f′(t)=8(1−t)3−3t2
f′(t)=0⇔8(1−t)3=3t2⇔8t2=3−9t+9t2−3t3⇔3t3−t2+9t−3=0⇔t=13
Bảng biến thiên của f(t)
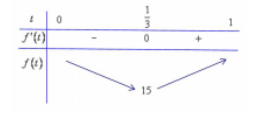
⇒minf(t)=f(13)=15⇒Pmin=15
Xem thêm các bài tiếp theo bên dưới
- Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân với $\lar
- Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị
- Số cách sắp xếp 6 bạn học sinh vào 6 ghế kê thành hàng ngang là . 60 1
- Diện tích mặt cầu có bán kính r=3 là 36π 18π $\L
- Điểm M trong hình vẽ bên biểu diễn số phức nào dưới đây? $\Large z=2-4