Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân với $\lar

Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân với $\large AB= AC= a$, góc $\large \widehat{BAC} = 120^\circ$, mặt phẳng (A'BC') tạo với đáy một góc $\large 60^\circ$. Tính thể tích V của khối lăng trụ đã cho

• A. A. $\large V= \dfrac{3a^3}{8}$
• B. B. $\large V= \dfrac{3\sqrt{3}a^3}{8}$
• C. C. $\large V= \dfrac{9a^3}{8}$
• D. D. $\large V= \dfrac{a^3\sqrt{3}}{8}$

Chọn B

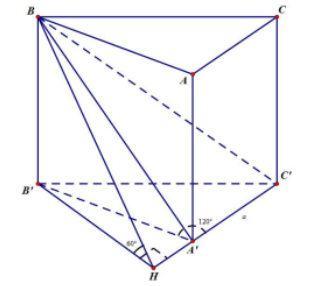
Trong mặt phẳng (A'B'C') kẻ $\large B'H'\perp A'C'\, (H\in A'C')$

Ta có: $\large \left\{\begin{align}& A'C'\perp B'H\\& A'C'\perp B'B\\\end{align}\right.$ $\large \Rightarrow A'C'\perp BH$ (định lý ba đường vuông góc) 

Có: $\large \left\{\begin{align}& (BA'C')\cap (A'B'C') = A'C'\\& BH\subset (BA'C'),\, BH\perp A'C'\\& B'H\subset (A'B'C'),\, B'H\perp A'C'\\\end{align}\right.$ $\large \Rightarrow \widehat{((BA'C'); (A'B'C')) }= \widehat{(BH, B'H)}= \widehat{BHB'}= 60^\circ$

Xét tam giác A'B'C' ta có: 

$\large S_{\Delta A'B'C}= \dfrac{1}{2}.A'B'. A'C'.\sin \widehat{B'A'C'}= \dfrac{1}{2}.B'H. A'C'\Rightarrow B'H= A'B'.\sin \widehat{B'A'C'}= \dfrac{a\sqrt{3}}{2}$

Xét tam giác BB'H vuông tại B' có: $\large B'B=B'H.\tan 60^\circ= \dfrac{3a}{2}$

Diện tích đáy: $\large S_{\Delta A'B'C'}= \dfrac{1}{2}.A'B'.A'C'.\sin \widehat{B'A'C'} = \dfrac{a^2\sqrt{3}}{4}$

Thể tích khối lăng trụ: $\large V_{ABC.A'B'C'}= BB'.S_{\Delta A'B'C'} = \dfrac{3a}{2}. \dfrac{a^2\sqrt{3}}{4} = \dfrac{3a^3\sqrt{3}}{8}$