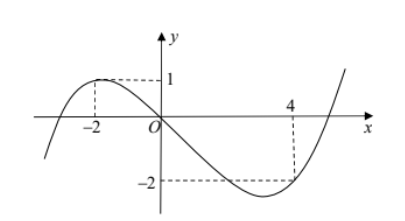
Cho hàm số f(x). Hàm số $\large y = f'(x) $ có đồ thị như hình bên. Hà

Cho hàm số f(x). Hàm số $\large y = f'(x) $ có đồ thị như hình bên. Hàm số $\large g(x) = f(1-2x)+x^2-x$ nghịch biến trên khoảng nào dưới đây?

• A. A. $\large \left( (1; \dfrac{3}{2}\right)$
• B. B. $\large (-2; 1)$
• C. C. $\large \left( (0; \dfrac{1}{2}\right)$
• D. D. $\large (2; 3)$

Chọn A

Ta có: $\large g(x) = f(1-2x) + x^2-x$

$\large \Rightarrow g'(x) = -2f'(1-2x) + 2x-1$

Để hàm số nghịch biến thì $\large g'(x) \leq 0\Leftrightarrow -2f'(1-2x) + 2x-1\leq 0\Leftrightarrow f'(1-2x) \geq \dfrac{2x-1}{2}$

Đặt $\large t= 1-2x$

Vẽ đường thẳng $\large y = -\dfrac{x}{2}$ và đồ thị hàm số $\large y= f'(x) $ trên cùng một hệ trục, ta có: 

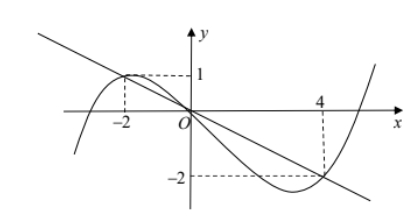
Hàm số g(x) nghịch biến $\large \Rightarrow g'(x) \leq 0\Rightarrow f'(t) \geq -\dfrac{1}{2} \Rightarrow $ $\large \left[\begin{align}& -2\leq t\leq 0\\& t\geq 4\\\end{align}\right. $

Như vậy $\large g'(1-2x)\geq \dfrac{1-2x}{2}\Leftrightarrow $ $\large \left[\begin{align}& -2\leq 1-2x\leq 0\\& 4\leq 1-2x\\\end{align}\right. $ $\large \Leftrightarrow \left[\begin{align}& \dfrac{1}{2}\leq x\leq \dfrac{3}{2}\\& x\leq -\dfrac{3}{2}\\\end{align}\right. $

Vậy hàm số $\large g(x)= f(1-2x) + x^2-x$ nghịch biến trên các khoảng $\large \left(-\infty; -\dfrac{3}{2}\right) $ và $\large \left(\dfrac{1}{2}; \dfrac{3}{2}\right) $

Mà $\large \left( 1; \dfrac{3}{2}\right) \subset \left( \dfrac{1}{2}; \dfrac{3}{2}\right) $ nên hàm số $\large $g(x) = f(1-2x) + x^2- x nghịch biến trên khoảng $\large \left( (1; \dfrac{3}{2}\right) $