Biết số phức z thỏa điều kiện $\Large 3 \leq|z-3 i+1| \leq 5$. Tập hợp

Biết số phức z thỏa điều kiện $\Large 3 \leq|z-3 i+1| \leq 5$. Tập hợp các điểm biểu diễn của z tọa thành một hình phẳn. Diện tích của hình phẳng đó bằng

• A. $\Large 16 \pi$
• B. $\Large 4 \pi$
• C. $\Large 9 \pi$
• D. $\Large 25 \pi$

Đặt $\Large z=x+y i$

$\Large |z-3 i-1|=|x-1+(y-3) t|=\sqrt{(x-1)^{2}+(y-3)^{2}}$

Do đó

$\Large 3 \leq|z-3 i+1| \leq 5 \Leftrightarrow 9 \leq(x-1)^{2}+(y-\beta)^{2} \leq 25$

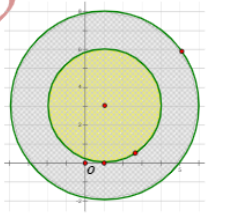
Tập hợp các điểm biểu diễn của Z là hình phẳn nằm trogn đường tròn tâm I(1;3) với bán kính bằng R=5 đồng thời nằm ngoài đường tròn tâm I(1;3) với bán kính r=3

Diện tích hình phẳng đó là

$\Large S=\pi .5^{2}-\pi .3^{2}=16 \pi$