Khái niệm đa giác. Đa giác đều
Lý thuyết về Khái niệm đa giác. Đa giác đều
1. Khái niệm đa giác
Định nghĩa: Đa giác lồi là đa giác luôn nằm trong một nửa mặt phẳng mà bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
2. Định nghĩa đa giác đều
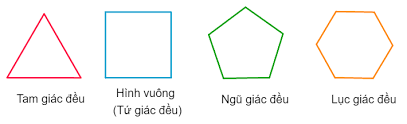
Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
Ví dụ về đa giác đều:
3. Góc trong đa giác
Tổng số đo các góc của đa giác n cạnh: $(n – 2). 180^0$
Số đo một góc của đa giác đều n cạnh: $\dfrac{(n-2){{.180}^{{}^\circ }}}{n}$
4. Số đường chéo của đa giác n cạnh
$\dfrac{n(n-3)}{2}$
Bài tập tự luyện có đáp án
Câu 1: Số trục đối xứng của ngũ giác đều là
- A
- B
- C
- D
Các đường thẳng qua đỉnh và tâm là các trục đối xứng của ngũ giác đều.
Khi đó ngũ giác đều có 5 trục đối xứng

Câu 2: Trong các hình sau có bao nhiêu hình là đa giác lồi




- A
- B
- C
- D
Các hình c, e, g là các đa giác lồi vì đa giác nằm trên một nửa mặt phẳng với bờ chứa bất kỳ cạnh nào của đa giác.
Câu 3:
Số đo mỗi góc của đa giác đều 8 cạnh bằng
- A
- B
- C
- D
Áp dụng: Hình n-giác đều có số đo môi góc bằng: $ \dfrac{\left( n-2 \right){{180}^{0}}}{n} $
Ta được số đo mỗi góc của đa giác đều 8 cạnh bằng: $ \dfrac{\left( 8-2 \right){{180}^{0}}}{8}={{135}^{0}} $
Câu 4: Số đường chéo của hình đa giác 8 cạnh là
- A
- B
- C
- D
Áp dụng: Hình n-giác có tất cả $ \dfrac{n\left( n-3 \right)}{2} $ đường chéo, ta được
Hình đa giác 10 cạnh có $ \dfrac{10\left( 10-3 \right)}{2}=35 $
Câu 5: Số đường chéo của hình đa giác 10 cạnh là
- A
- B
- C
- D
Áp dụng: Hình n-giác có tất cả $ \dfrac{n\left( n-3 \right)}{2} $ đường chéo, ta được
Hình đa giác 10 cạnh có $ \dfrac{10\left( 10-3 \right)}{2}=35 $
Câu 6: Cho $ ABCDEF $ là hình lục giác đều. Hãy chọn câu sai.
- A
- B
- C
- D
Số đo góc trong của hình lục giác đều: $ \dfrac{(6-2){{.180}^{0}}}{6}={{120}^{\circ }} $
Tổng số đo góc trong của lục giác đều là: $ (6-2){{.180}^{0}}={{720}^{0}}. $
Câu sai là: Mỗi góc trong của nó là $ {{150}^{\circ }} $ .
Câu 7: Tổng số đo các góc trong của hình đa giác $ n $ cạnh là $ 1440{}^\circ $ thì số cạnh $ n $ là:
- A
- B
- C
- D
Từ giả thiết ta có $ (n-2){{.180}^{\circ }}={{1440}^{\circ }}\Leftrightarrow n-2=8\Leftrightarrow n=10 $ .
Câu 8: Số đo mỗi góc của đa giác đều 12 cạnh bằng
- A
- B
- C
- D
Áp dụng: Hình n-giác đều có số đo môi góc bằng: $ \dfrac{\left( n-2 \right){{180}^{0}}}{n} $
Ta được số đo mỗi góc của đa giác đều 12 cạnh bằng: $ \dfrac{\left( 12-2 \right){{180}^{0}}}{12}={{150}^{0}} $
Câu 9: Số trục đối xứng của lục giác đều là
- A
- B
- C
- D
Các đường thẳng qua tâm và các đỉnh+ các đường thẳng qua trung điểm của 2 cạnh đối diện đều là trục đối xứng của lục giác đều
Khi đó lục giác đều có 6 trục đối xứng

Câu 10: Một đa giác có số đường chéo là $ 54 $ thì có số cạnh là
- A
- B
- C
- D
Ta có:
$ \begin{array}{l} \dfrac{n(n-3)}{2}=54\Leftrightarrow {{n}^{2}}-3n-108=0\Leftrightarrow (n-12)(n+9)=0 \\ \Leftrightarrow \left[ \begin{array}{l} n-12=0 \\ n+9=0 \end{array} \right.\Leftrightarrow \left[ \begin{array}{l} n=12(tm) \\ n=-9(ktm) \end{array} \right. \end{array} $
Số cạnh của đa giác là $ 12 $ .
Xem thêm các bài tiếp theo bên dưới