Diện tích hình thang
Lý thuyết về Diện tích hình thang
Công thức tính diện tích hình thang
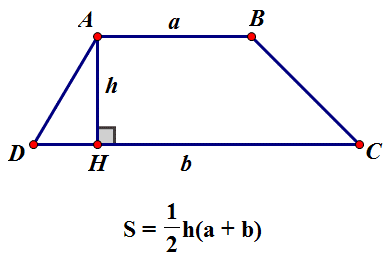
Diện tích hình thang bằng một nửa tích của tổng hai đáy với chiều cao.
$S=\dfrac{1}{2}(a+b).h$
Bài tập tự luyện có đáp án
Câu 1: Cho hình vẽ bên dưới. Số hình có cùng diện tích với hình bình hành $FIGE$ trong hình vẽ là


- A
- B
- C
- D
Ta có: $ IG//FU $ nên khoảng cách giữa hai đường thẳng IG và FU không đổi và bằng h.
Các hình bình hành $ FIGE,IGRE,IGUR $ có cạnh bằng nhau $ FE=ER=RU $ có cùng chiều cao ứng với cạnh đó nên diện tích chúng bằng nhau.
Tức là $ {{S}_{FIGE}}~={{S}_{IGRE}}~={{S}_{IGUR}}=h.FE $
Mặt khác các tam giác IFR, GEU có cạnh đáy FR và EU bằng nhau, bằng hai lần cạnh hình bình hành FIGE và có cùng chiều cao với chiều cao hình bình hành FIGE nên diện tích chúng bằng nhau.
$ {{S}_{IFR}}~={{S}_{GEU}}~={{S}_{FIGE}} $
Vậy $ {{S}_{FIGE}}~={{S}_{IGRE}}~={{S}_{IGUR}}~={{S}_{IFR}}~={{S}_{GEU}} $
Câu 2: Cho hình thang ABED như hình vẽ. Biết chu vi hình chữ nhật $ ABCD $ bằng $ 118 $ m. Khi đó diện tích hình thang ABED bằng


- A
- B
- C
- D
Ta có chu vi ABCD bằng:
$ \begin{array}{l} \left( AB+BC \right)2=118\Rightarrow BC=36m \\ \Rightarrow {{S}_{ABED}}=\dfrac{\left( AB+DE \right)BC}{2}=\dfrac{\left( 23+31 \right)36}{2}=972{{m}^{2}} \end{array} $
Câu 3: Cho hình thang $ABCD$ vuông tại A và D, biết $ AB=4cm,CD=6cm $ , góc tạo bởi một cạnh bên và đáy lớn có số đo bằng $ {{45}^{0}} $ . Diện tích hình thang ABCD bằng
- A
- B
- C
- D

Dựng $ BE\bot CD $ tại E
Ta có $ EC=6-4=2cm $
Do cạnh bên hợp với đáy lớn 1 góc $ {{45}^{0}} $ nên ta có góc $ \widehat{C}={{45}^{0}} $
Có tam giác $ EBC $ vuông tại E nên tam giác $ EBC $ là tam giác vuông cân tại E
$ \Rightarrow BE=EC=2cm $
Khi đó $ {{S}_{ABCD}}=\dfrac{\left( AB+CD \right)BE}{2}=\dfrac{\left( 4+6 \right)2}{2}=10c{{m}^{2}} $
Câu 4: Cho hình thang $ ABCD,BC//AD $ . Các đường chéo cắt nhau tại O. Khi đó
- A
- B
- C
- D

Vì $ BC//AD\left( gt \right)\Rightarrow $ Chiều cao hạ từ B và C cùng xuống AD bằng nhau.
$ \Rightarrow {{S}_{BAD}}={{S}_{CAD}} $ $ \Rightarrow {{S}_{OAB}}+{{S}_{OAD}}={{S}_{OCD}}+{{S}_{OAD}} $
Vậy $ {{S}_{OAB}}={{S}_{OCD}} $ .
Câu 5: Cho hình bình hành ABCD có diện tích S. Trên cạnh BC lấy hai điểm M, N sao cho $ BM=MN=NC=\dfrac{1}{3}BC $ . Diện tích của tứ giác ABMD theo S là
- A
- B
- C
- D

Có $ CM=\dfrac{2}{3}BC $
Hình bình hành $ ABCD $ và $ \Delta DMC $ có chung đường cao kẻ từ đỉnh D đến BC.
Gọi khoảng cách giữa AD và BC là $ h,BC=a $
Ta có diện tích hình bình hành $ ABCD $ là $ S=ah $
$ {{S}_{DMC}}=\dfrac{1}{2}h.\dfrac{2}{3}a=\dfrac{1}{3}ah=\dfrac{1}{3}S $
$ {{S}_{ABMD}}={{S}_{ABCD}}-{{S}_{DMC}}=S-\dfrac{1}{3}S=\dfrac{2}{3}S $
Cách 2: Ta có $ BM=\dfrac{1}{3}a $
$ \Rightarrow {{S}_{ABMD}}=\dfrac{\left( BM+AD \right)h}{2}=\dfrac{\left( \dfrac{1}{3}a+a \right)h}{2}=\dfrac{2}{3}ah=\dfrac{2}{3}S $
Câu 6: Diện tích hình thang ABCD, đáy lớn AB = 8cm, đáy nhỏ CD = 6cm và đường cao DH= 5cm là
- A
- B
- C
- D
Sử dụng công thức tính diện tích hình thang ta được
$ {{S}_{ABCD}}=\dfrac{\left( AB+CD \right)DH}{2}=\dfrac{\left( 8+6 \right)5}{2}=35\left( c{{m}^{2}} \right) $
Câu 7: Cho hình hành ABCD, có AD=8cm và AB=9cm. Đường cao AH xuống DC có độ dài là 6cm. Đường cao AK đến BC . Tính độ dài đường cao AK.
- A
- B
- C
- D

Ta có: $ {{S}_{ABCD}}=AH.CD=6.9=54\left( c{{m}^{2}} \right) $
$ {{S}_{ABCD}}=AK.BC=8.AK $
Suy ra: $ 8.AK=54\Rightarrow AK=\dfrac{54}{8}=\dfrac{27}{4}\left( cm \right) $
Câu 8: Cho tam giác ABC vuông tại A. Về phía ngoài tam giác, vẽ các hình vuông $ ABDE,ACFG,BCHI $ . Chọn khẳng định đúng.
- A
- B
- C
- D
Ta có $ {{S}_{BCHI}}=B{{C}^{2}};{{S}_{ACFG}}=A{{C}^{2}};{{S}_{ABDE}}=A{{B}^{2}} $ Theo định lý Pytago cho tam giác $ ABC $ vuông tại $ A $ ta có: $ B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}\Rightarrow {{S}_{BCHI}}={{S}_{ACFG}}+{{S}_{ABDE}} $ .
Câu 9: Tính diện tích mảnh đất hình thang vuông $ ABCD $ có độ dài hai đáy $ AB=10cm;DC=13cm;\widehat{A}=\widehat{D}=90{}^\circ $ (hình vẽ), biết tam giác $ BEC $ vuông tại $ E $ và có diện tích bằng $ 13,5c{{m}^{2}} $ . 
- A
- B
- C
- D
Tứ giác $ ABED $ có $ \hat{A}=\hat{D}=\hat{E}={{90}^{\circ }} $ nên là hình chữ nhật.
Suy ra $ DE=AB=10cm $ Do đó: $ \,EC=DC-DE=13-10=3(cm) $
Ta có:
$ \begin{array}{l} {{S}_{BEC}}=\dfrac{1}{2}BE.EC\Rightarrow BE=\dfrac{2{{S}_{BEC}}}{EC}=\dfrac{2.13,5}{3}=9(cm) \\ {{S}_{ABED}}=AB.BE=10.9=90(c{{m}^{2}}) \\ {{S}_{ABCD}}={{S}_{ABED}}+{{S}_{BEC}}=90+13,5=103,5(c{{m}^{2}}). \end{array} $
Câu 10: Cho hình vẽ dưới đây với $ ABCD $ là hình chữ nhật, $ MNCB $ là hình bình hành. Chọn khẳng định đúng. 
- A
- B
- C
- D
Vì $ ABCD $ là hình chữ nhật nên $ {{S}_{ABCD}}=BC.DC $
Vì $ BCNM $ là hình bình hành, lại có $ CD\bot AD $ (vì $ ABCD $ là hình chữ nhật) hay $ CD\bot MN $ nên ta có: $ {{S}_{BCNM}}=MN.DC $
Mà $ BC=MN $ (do $ BCNM $ là hình bình hành) nên $ {{S}_{BCNM}}=MN.DC=BC.CD $ , suy ra $ {{S}_{ABCD}}={{S}_{BCNM}} $ .
Câu 11: Cho hình bình hành $ABCD$ có diện tích $S$. Trên cạnh $BC$ lấy hai điểm $M, N$ sao cho $ BM=MN=NC=\dfrac{1}{3}BC $ . Từ M kẻ đường thẳng $//AB$ cắt $AD$ tại $E$. Diện tích của tứ giác $ABNE$ theo $S$ là
- A
- B
- C
- D

Gọi khoảng cách giữa AD và BC là $ h,BC=a $
Ta có diện tích hình bình hành $ ABCD $ là $ S=ah $
$ \begin{array}{l} AE=BM=\dfrac{1}{3}BC=\dfrac{1}{3}a \\ BN=\dfrac{2}{3}BC=\dfrac{2a}{3} \\ \Rightarrow {{S}_{ABNE}}=\dfrac{\left( AE+BN \right)h}{2}=\dfrac{ah}{2}=\dfrac{S}{2} \end{array} $