Trường hợp góc – cạnh – góc (g.c.g)
Lý thuyết về Trường hợp góc – cạnh – góc (g.c.g)
3. Trường hợp góc – cạnh – góc (g.c.g)
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và góc kề của tam giác kìa thì hai tam giác đó bằng nhau.
ΔABCΔABC và ΔA′B′C′ có:
{ˆB=^B′BC=B′C′ˆC=^C′
⇒ΔABC=ΔA′B′C′
– Hệ quả 1: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
– Hệ quả 2. Nếu cạnh huyền và góc nhọn của tam giác vuông nay bằng cạnh huyền, góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Bài tập tự luyện có đáp án
Câu 1: Cho hình vẽ bên. 
Số đo góc MQN là
Số đo góc MQN là
- A
- B
- C
- D
Áp dụng định lí pytago trong tam giác vuông ΔMNP và ΔNMQ dễ dàng ta có NQ=PM
Xét ΔMNP và ΔNMQ có {NP=MQNQ=PMMNchung⇒ΔMNP=ΔNMQ(c.c.c)⇒^MQN=^NPM=48o
Câu 2: Cho tam giác ABC có ˆB=ˆC . Tia phân giác của góc B cắt AC ở D. Tia phân giác của góc C cắt AB ở E. Khi đó
- A
- B
- C
- D

Vì BD là tia phân giác của ^ABC nên ^CBD=12^ABC .
Vì CE là tia phân giác của ^ACB nên ^BCE=12^ACB .
Mà ^ABC=^ACB (theo giả thiết)
Do đó: ^CBD=^BCE .
Xét tam giác BEC và tam giác CDB có:
^EBC=^DCB (giả thiết); Cạnh BC chung; ^BCE=^CBD (chứng minh trên)
⇒ΔBEC=ΔCDB(g.c.g)
⇒CE=BD;BE=CD .
Câu 3: Cho hình vẽ sau, trong đó AB//CD;AB=CD. 
Khẳng định nào sau đây là đúng ?

Khẳng định nào sau đây là đúng ?
- A
- B
- C
- D
Vì AB // CD nên ^OAB=^OCD (so le trong); ^OBA=^ODC (so le trong).
Xét tam giác AOB và tam giác COD có:
^OAB=^OCD (chứng minh trên);
AB=CD (giả thiết)
^OBA=^ODC (chứng minh trên)
⇒ΔAOB=ΔCOD(g.c.g)
⇒OA=OC,OB=OD.
Câu 4: Cho tam giác ABC có M là trung điểm của AB. Từ M kẻ MI song song với BC (I thuộc AC). Từ I kẻ IK song song với AB (K thuộc BC). Hỏi AB gấp mấy lần IK?
- A
- B
- C
- D

Xét tam giác BMK và tam giác IKM có
^IMK=^MKB (so le trong do MI // BC);
Cạnh MK chung;
^BMK=^MKI (so le trong do BM // IK)
⇒ΔBMK=ΔIKM(g.c.g)⇒IK=BM . (1)
Vì M là trung điểm của AB nên AM=BM . (2)
Từ (1) và (2) suy ra IK=AM=12AB .
Câu 5: Trong hình vẽ dưới đây, 
ta có AD // BC; AB // CD. Khẳng định nào dưới đây là đúng ?
ta có AD // BC; AB // CD. Khẳng định nào dưới đây là đúng ?
- A
- B
- C
- D
Ta có AD // BC nên ^CBD=^BDA
AB // CD nên ^ABD=^BDC
Xét ΔABD và ΔCDB có
{^CBD=^BDA^ABD=^BDCBDchung⇒ΔABD=ΔCDB(g.c.g)⇒{AB=CDAD=BC
Câu 6: Cho hình vẽ sau: 
Kết luận nào sau đây không đúng ?

Kết luận nào sau đây không đúng ?
- A
- B
- C
- D
Xét tam giác ABC có: ˆA+ˆB+ˆC=180o
⇒ˆC=180o−(ˆA+ˆB)=180o−(80o+60o)=40o .
Xét tam giác MNP có: ˆM+ˆN+ˆP=180o
⇒ˆP=180o−(ˆM+ˆN)=180o−(80o+40o)=60o .
Xét tam giác ABC và tam giác MPN có:
ˆA=ˆM=80o ; AC=MN (giả thiết) ; ˆC=ˆN=40o
⇒ΔABC=ΔMPN(g.c.g)⇒AB=MP;BC=NP.
Câu 7: Cho hình vẽ sau, trong đó: BM là tia phân giác của ^ABC . 
Biết rằng ^ABC=50o ; ^BAM=^BCM=30o . Khi đó có thể chứng minh ΔABM=ΔCBM theo trường hợp nào sau đây ?

Biết rằng ^ABC=50o ; ^BAM=^BCM=30o . Khi đó có thể chứng minh ΔABM=ΔCBM theo trường hợp nào sau đây ?
- A
- B
- C
- D
Vì BM là tia phân giác của ^ABC nên ^ABM=^CBM=12^ABC=12.50o=25o .
Xét tam giác ABM có: ^BAM+^ABM+^AMB=180o
⇒^AMB=180o−(^BAM+^ABM)=180o−(30o+25o)=125o .
Xét tam giác BCM có: ^BMC+^MBC+^MCB=180o
⇒^BMC=180o−(^MBC+^MCB)=180o−(25o+30o)=125o .
Xét tam giác ABM và tam giác CBM có:
^ABM=^CBM ; Cạnh BM chung ; ^AMB=^CMB=125o
⇒ΔABM=ΔCBM(g.c.g).
Câu 8: Cho tam giác ABC có AD là đường phân giác của ^BAC (D thuộc BC). Nếu AD vuông góc với BC thì kết luận nào sau đây là sai?
- A
- B
- C
- D

Xét tam giác ABD và tam giác ACD có:
^BAD=^CAD (Vì AD là tia phân giác của ^BAC );
Cạnh AD chung;
^ADB=^ADC=90o
⇒ΔABD=ΔACD (g.c.g)
⇒AB=AC;BD=CD;ˆB=ˆC .
Ta có: AD⊥BC,BD=CD ⇒ AD là đường trung trực của BC.
Câu 9: Cho hình vẽ sau, trong đó AM // BN, IM = IN. 
Khẳng định nào sau đây là sai?

Khẳng định nào sau đây là sai?
- A
- B
- C
- D
Xét tam giác AMI và tam giác BNI có:
^AIM=^BIN (đối đỉnh);
IM=IN (giả thiết);
^AMI=^BNI (so le trong do AM // BN)
⇒ΔAMI=ΔBNI(g.c.g)
⇒AM=BN;AI=BI
Vì AI=BI và I nằm giữa A và B nên I là trung điểm của AB.
Vì ΔAMI=ΔBNI nên hai tam giác AIM và BIN có diện tích bằng nhau.
Câu 10: Cho tam giác ABC. Trên tia đối của tia CB lấy điểm E sao cho CE = CB. Từ E kẻ đường thẳng song song với AB cắt tia AC tại F. Nối A với E, B với F, E với F. Hỏi trong hình vẽ có bao nhiêu cặp tam giác bằng nhau?
- A
- B
- C
- D

Vì BF // AB nên ^ABC=^CEF (so le trong).
Xét tam giác ABC và tam giác FEC có:
^ABC=^CEF ; BC = CE (giả thiết) ; ^ACB=^FCE (đối đỉnh).
⇒ΔABC=ΔFEC(g.c.g)
⇒AC=CF.
Xét tam giác ACE và tam giác BCF có:
AC = CF (chứng minh trên); CE = BC ; ^ACE=^BCF (đối đỉnh)
⇒ΔACE=ΔFCB(c.g.c)
Xét tương tự ta có: ΔABE=ΔFEB;ΔAEF=ΔFBA .
Vậy có 4 cặp tam giác bằng nhau.
Câu 11: Cho hình vẽ sau: 
Nếu BE=13AB thì chu vi tam giác AFC bằng bao nhiêu?

Nếu BE=13AB thì chu vi tam giác AFC bằng bao nhiêu?
- A
- B
- C
- D
Ta có: ^AEF+^AEB=180o (kề bù);
^AFE+^AFC=180o (kề bù);
Mà ^AEF=^AFE (giả thiết)
⇒^AEB=^AFC .
Xét tam giác ABE và tam giác ACF có:
^ABE=^ACF (giả thiết);
BE = CF (giả thiết);
^AEB=^AFC
⇒ΔABE=ΔACF(g.c.g)
⇒AC=AB=12cm;AF=AE=9cm;
FC=BE=13AB=13.12=4cm.
Vậy chu vi tam giác AFC là: AF+AC+FC=9+12+4=25(cm).
Câu 12: Cho hình bên 
Khẳng định sai là
Khẳng định sai là
- A
- B
- C
- D
Xét tam giác SKH có ^SHK+^SKH+^KSH=180o⇒^SKH=50o
Tương tự ta có ^HKI=50o
Xét ΔSHK và ΔIHK có {^SHK=^IHK^SKH=^IKHHKchung⇒ΔSHK=ΔIHK(g.c.g)
Nên KH là tia phân giác ^SKI ; HS=HI; SK= IK
Câu 13: Cho hình vẽ sau, trong đó AB//CD,AD//BC . 
Hệ thức bằng nhau giữa hai tam giác theo thứ tự đỉnh tương ứng nào sau đây là đúng?

Hệ thức bằng nhau giữa hai tam giác theo thứ tự đỉnh tương ứng nào sau đây là đúng?
- A
- B
- C
- D
+ Xét tam giác ABD và tam giác CDB có:
^ABD=^BDC (so le trong do AB // CD);
Cạnh BD chung;
^ADB=^CBD (so le trong do AD // BC)
⇒ΔABD=ΔCDB(g.c.g) .
+ Xét tam giác ABC và tam giác CDA có:
^BAC=^ACD (so le trong do AB // CD);
Cạnh AC chung;
^ACB=^DAC (so le trong do AD // BC)
⇒ΔABC=ΔCDA(g.c.g) .
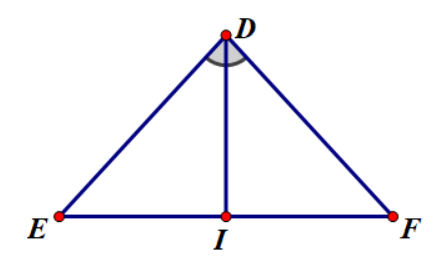
Câu 14: Chọn khẳng định sai. Cho tam giác DEF có ˆE=ˆF . Tia phân giác của góc D cắt EF tại I . Ta có
Cho tam giác DEF có ˆE=ˆF . Tia phân giác của góc D cắt EF tại I . Ta có
- A
- B
- C
- D

Xét ΔDEF có ˆE=ˆF nên DE=DF nên ΔDEF cân tại D
Mà DI là tia phân giác của ^EDF⇒^EDI=^IDF và DI là đường trung tuyến, đường cao của ΔDEF⇒FI=EI
Xét ∆ DIE và ∆ DIF có EI=FI; DE=DF; cạnh DI chung nên ∆ DIE = ∆ DIF
Câu 15: Cho Δ ABC có ˆB=ˆC .Tia phân giác của góc A cắt BC tại D. Khẳng định đúng là
- A
- B
- C
- D
Cho Δ ABC có ˆB=ˆC nên AC=AB
Do AD là tia phân giác của góc ^BAC nên ^BAD=^CAD
Xét ΔABD và ΔACD có
^BAD=^CAD
ˆB=ˆC
AB=AC
Nên ΔABD=ΔACD (g.c.g)
Câu 16: Cho góc nhọn xOy và K là một điểm thuộc tia phân giác của góc xOy. Kẻ KA vuông góc với Ox (A ∈ Ox), KB vuông góc với Oy ( B ∈ Oy). Khẳng định nào sai?
- A
- B
- C
- D

Xét ΔOBK và ΔOAK có
^BOK=^AOK ( OK là phân giác góc xOy)
Cạnh OK chung;
^KBO=^KAO=90o
⇒ΔOBK=ΔOAK⇒^BKO=^AKO nên OK là phân giác góc AK ⇒OK⊥AB
Câu 17: Chọn câu trả lời đúng. 
Nếu thêm điều kiện để hai tam giác trong hình vẽ bên là hai tam giác bằng nhau theo trường hợp góc – cạnh – góc?
Nếu thêm điều kiện để hai tam giác trong hình vẽ bên là hai tam giác bằng nhau theo trường hợp góc – cạnh – góc?
- A
- B
- C
- D
Để ΔFGE=ΔGFH(g.c.g) thì ^EGF=^GFH⇒EG//FH
Xem thêm các bài tiếp theo bên dưới