Các đại lượng đặc trưng của con lắc lò xo
Lý thuyết về Các đại lượng đặc trưng của con lắc lò xo
1. Tần số góc trong dao động của con lắc lò xo
Tần số góc: $\omega =\sqrt{\dfrac{k}{m}}$
2. Tần số
tần số: $f=\frac{1}{T}=\dfrac{\omega }{2\pi }=\frac{1}{2\pi }\sqrt{\dfrac{k}{m}}$=$\dfrac{1}{2\pi }\sqrt{\dfrac{\Delta \ell }{g}}$
3. Chu kì
chu kỳ: $T=\dfrac{2\pi }{\omega }=2\pi \sqrt{\dfrac{m}{k}}$=$2\pi \sqrt{\dfrac{\Delta l}{g}}$
Trong đó:
f là tần số sao động (Hz)
T là chu kì dao động (s)
$\omega $ là tần số góc (rad/s)
$\Delta {{l}_{}}$ là độ biến dạng của lò xo ở VTCB(m)
m là khối lượng của vật(kg)
k là độ cứng của lò xo(N/m)
g là gia tốc trọng trường $\left( g\approx 10m/{{s}^{2}} \right)$
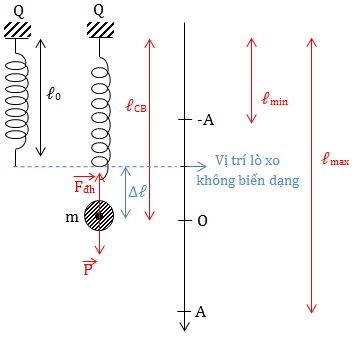
3. Biên độ CLLX
+ Chiều dài lò xo tại VTCB: ${{l}_{CB}}={{l}_{0}}+\Delta l$ (l0 là chiều dài tự nhiên;$\Delta {{l}_{}}$ là độ biến dạng của lò xo ở VTCB(m))
+ Chiều dài cực tiểu (khi vật ở vị trí cao nhất): ${{l}_{Min}}={{l}_{0}}+\Delta l+A$
+ Chiều dài cực đại (khi vật ở vị trí thấp nhất): ${{l}_{Max}}={{l}_{0}}+\Delta l+A$
$A=\dfrac{{{l}_{Min}}-{{l}_{Max}}}{2}$
Bài tập tự luyện có đáp án
Câu 1: Nếu gọi v, a và ω lần lượt là vận tốc, gia tốc và tần số góc của con lắc lò xo. Biểu thức liên hệ nào dưới đây giữa biên độ A với các đại lượng trên là đúng:
- A
- B
- C
- D
Ta có: $ \dfrac{{{v}^{2}}}{{{\omega }^{2}}{{A}^{2}}}+\dfrac{{{a}^{2}}}{{{\omega }^{4}}{{A}^{2}}}=1\Rightarrow A=\sqrt{\dfrac{{{v}^{2}}}{{{\omega }^{2}}}+\dfrac{{{a}^{2}}}{{{\omega }^{4}}}} $
Câu 2: Vật nặng m=200g gắn vào một lò xo. Con lắc này dao động với tần số f=10Hz. Lấy $ {{\pi }^{2}}=10 $ . Lò xo có độ cứng:
- A
- B
- C
- D
Tần số:
$ f=\dfrac{1}{2\pi }\sqrt{\dfrac{k}{m}}\Rightarrow k=4{{\pi }^{2}}{{f}^{2}}.m=800\left( N/m \right) $
Câu 3: Treo một vật có khối lượng 1 kg vào một lò xo có độ cứng k = 98N/m. Kéo vật ra khỏi vị trí cân bằng về phía dưới đến vị trí x = 5cm rồi thả nhẹ. Gia tốc cực đại của vật dao động điều hoà là
- A
- B
- C
- D
$ \omega =\sqrt{\dfrac{k}{m}}=7\sqrt{2}\left( rad/s \right) $
Kéo vật ra khỏi vị trí cân bằng về phía dưới đến vị trí x = 5cm rồi thả nhẹ $ \Rightarrow A=5cm $
$ \Rightarrow {{a}_{\max }}={{\omega }^{2}}A=4,9\left( m/{{s}^{2}} \right) $
Câu 4: Một con lắc lò xo gồm một lò xo treo thẳng đứng có đầu trên gắn cố định, đầu dưới gắn vật nặng m, kích thích cho m dao động thẳng đứng thì nó dao động điều hòa có tần số góc 10 rad/s. Lấy \[ g=10m/{{s}^{2}} \] . Tại vị trí cân bằng độ dãn của lò xo là
- A
- B
- C
- D
$ \omega =\sqrt{\dfrac{g}{\Delta \ell }}\Rightarrow \Delta \ell =\dfrac{g}{{{\omega }^{2}}}=0,1m=10cm $
Câu 5: Vật có khối lượng 0,5kg treo vào lò xo có k=80(N/m). Dao động theo phương thẳng đứng với biên độ 5(cm). Gia tốc cực đại của vật là :
- A
- B
- C
- D
$ \omega =\sqrt{\dfrac{k}{m}}=4\pi \left( ra\text{d}/s \right) $ $ \Rightarrow {{a}_{\max }}={{\omega }^{2}}A=8\left( m/{{s}^{2}} \right) $
Câu 6: Treo một vật nặng vào một lò xo, tại vị trí cân bằng lò xo dãn 5cm, lấy $ g=10m/{{s}^{2}} $ . Kích thích cho vật dao động với biên độ nhỏ thì chu kỳ dao động của vật là
- A
- B
- C
- D
$ \Delta \ell =5cm\Rightarrow T=2\pi \sqrt{\dfrac{\Delta \ell }{g}}=0,44\text{s} $
Câu 7: Một vật nặng treo vào một đầu lò xo làm cho lò xo dãn ra 1,6 cm. Đầu kia treo vào một điểm cố định O. Hệ dao động điều hòa theo phương thẳng đứng. Cho biết \[ g=10m/{{s}^{2}} \] .Tìm chu kỳ dao động của hệ.
- A
- B
- C
- D
$ \Delta \ell =1,6cm\Rightarrow T=2\pi \sqrt{\dfrac{\Delta \ell }{g}}=0,25\text{s} $
Câu 8: Một con lắc lò xo thẳng đứng gồm một vật khối lượng m treo vào lò xo. Độ biến dạng của lò xo khi ở vị trí cân bằng là $ \Delta l $ . Chu kì dao động của co lắc lò xo là :
- A
- B
- C
- D
Chu kì của con lắc lò xo: $ T=2\pi \sqrt{\dfrac{\Delta l}{g}} $
Câu 9: Một con lắc lò xo treo thẳng đứng, độ cứng k = 100 N/m, vật nặng khối lượng m = 500 g. Khi vật cân bằng lò xo dãn:
- A
- B
- C
- D
Áp dụng công thức tính độ dãn của lò xo đứng khi ở cân bằng $ \Delta l=\dfrac{mg}{k} $
Khi ở vị trí cân bằng lò xo dãn một đoan bằng $ \Delta l=\dfrac{mg}{k}=\dfrac{0,5\cdot 10}{100}=0,05m=5cm $
Câu 10: Một con lắc lò xo treo thẳng đứng, tại vị trí cân bằng người ta thấy lò xo bị dãn 10cm. Lấy $ g=10m/{{s}^{2}} $ . Chu kì và tần số của con lắc là:
- A
- B
- C
- D
$ \Delta \ell =10cm\Rightarrow T=2\pi \sqrt{\dfrac{\Delta \ell }{g}}=0,2\pi \left( s \right)\Rightarrow f=\dfrac{5}{\pi }\left( H\text{z} \right) $
Câu 11: Phát biểu nào sau đây không đúng với con lắc lò xo ngang?
- A
- B
- C
- D
Chuyển động của con lắc lò xo nằm ngang không phải là chuyển động biến đổi đều vì gia tốc của vật thay đổi.
Câu 12: Phát biểu nào sau đây là sai khi nói về dao động trên phương ngang của con lắc lò xo khối lượng m, độ cứng k?
- A
- B
- C
- D
Chu kì dao động phụ thuộc vào độ cứng k và khối lượng m mà không phụ thuộc vào biên độ dao động.
Câu 13: Tần số dao động của con lắc lò xo sẽ tăng khi
- A
- B
- C
- D
Tần số: $ f=\dfrac{1}{2\pi }\sqrt{\dfrac{k}{m}} $
Tần số tăng khi tăng độ cứng và giữ nguyên khối lượng của con lắc.
Câu 14: Một vật khối lượng 10kg được treo vào đầu một lò xo có khối lượng không đáng kể có độ cứng 40N/m. Tìm tần số góc $ \omega $ vào tần số của dao động điều hoà của vật
- A
- B
- C
- D
$ \omega =\sqrt{\dfrac{k}{m}}=2\left( rad/s \right)\Rightarrow f=\dfrac{\omega }{2\pi }=0,32\left( Hz \right) $
Câu 15: Một con lắc lò xo nằm ngang lò xo nhẹ có độ cứng k=100N/m và vật nhỏ có khối lượng m=100g. Kích thích cho con lắc dao động, lấy $ \pi =\sqrt{10} $ . Tần số của con lắc là:
- A
- B
- C
- D
$ f=\dfrac{1}{2\pi }\sqrt{\dfrac{k}{m}}=5\left( H\text{z} \right) $
Câu 16: Một con lắc lò xo treo thẳng đứng với vật có khối lượng m=1kg, lò xo nhẹ có độ cứng k=100N/m. Kéo vật ra khỏi vị trí cân bằng, về phía dưới đến cách vị trí cân bằng x=5cm rồi thả ra. Gia tốc cực đại của dao động điều hòa của vật là:
- A
- B
- C
- D
$ \omega =\sqrt{\dfrac{k}{m}}=10\left( rad/s \right) $
Kéo vật ra khỏi vị trí cân bằng, về phía dưới đến cách vị trí cân bằng x=5cm rồi thả ra $ \Rightarrow A=5cm $
$ \Rightarrow {{a}_{\max }}={{\omega }^{2}}A=500\left( cm/{{s}^{2}} \right)=5\left( m/{{s}^{2}} \right) $
Câu 17: Một con lắc lò xo gồm viên bi nhỏ có khối lượng m và lò xo khối lượng không đáng kể có độ cứng k, dao động điều hoà theo phương thẳng đứng tại nơi có gia tốc rơi tự do là g. Khi viên bi ở vị trí cân bằng, lò xo dãn một đoạn ∆ℓ . Tần số góc dao động của con lắc này là
- A
- B
- C
- D
$\omega =\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{g}{\Delta \ell }}$
Câu 18: Một con lắc lò xo bố trí dao động trên mặt phẳng nghiêng . Góc $ \alpha $ là góc hợp bới mặt phẳng nghiêng và mặt ngang cho $ \alpha ={{30}^{0}} $ , $ g=10m/{{s}^{2}},{{\pi }^{2}}=10 $ . Kích thích cho vật dao động thì chu kì của con lắc là $ T=0,4s $ . Độ dãn của lò xo tại vị trí cân bằng là:
- A
- B
- C
- D
$ T=2\pi \sqrt{\dfrac{\Delta \ell }{g\sin \alpha }}\Rightarrow \Delta \ell =\dfrac{{{T}^{2}}g\sin \alpha }{4{{\pi }^{2}}}=0,02m=2cm $
Xem thêm các bài tiếp theo bên dưới