Hình thoi
Lý thuyết về Hình thoi
Định nghĩa: Hình thoi là tứ giác có bốn cạnh bằng nhau.
$ABCD$ là hình thoi $\Leftrightarrow$ $ABCD$ là tứ giác có $AB = BC = CD = DA$.
Tính chất: Trong hình thoi:
- Hai đường chéo vuông góc với nhau.
- Hai đường chéo là các đường phân giác các góc của hình thoi.
Dấu hiệu nhận biết hình thoi.
- Tứ giác có bốn cạnh bằng nhau là hình thoi.
- Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
- Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
- Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
Bài tập tự luyện có đáp án
Câu 1: Trong các khẳng định sau, khẳng định nào sai đối với hình thoi là
- A
- B
- C
- D
Hai đường chéo của hình thoi chưa chắc đã bằng nhau, nhưng luôn vuông góc với nhau tại trung điểm của mỗi đường và là tia phân giác của các góc hình thoi.
Câu 2: Hãy chọn câu sai.
- A
- B
- C
- D
+ Tứ giác có bốn cạnh bằng nhau là hình thoi.
+ Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
+ Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi..
+ Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
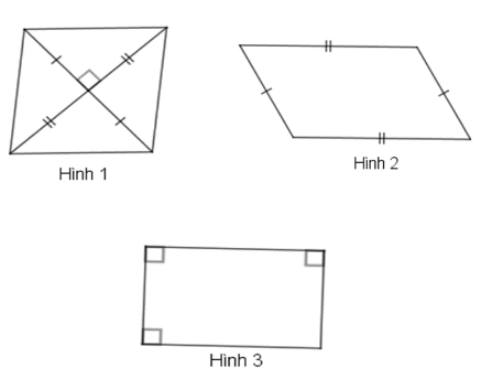
Câu 3: Cho các hình sau, chọn khẳng định đúng.


- A
- B
- C
- D
Hình 1 là hình thoi vì có hai đường chéo giao nhau tại trung điểm mỗi đường và vuông góc với nhau.
Hình 2 không là hình thoi vì bốn cạnh không bằng nhau.
Hình 3 không là hình thoi vì bốn cạnh không bằng nhau.
Câu 4: Khẳng định đúng là
- A
- B
- C
- D
Câu 5: Khẳng định sai là
- A
- B
- C
- D
Hình thoi có hai trục đối xứng chính là hai đường chéo của nó.
Câu 6: Hình thoi không có tính chất nào dưới đây?
- A
- B
- C
- D
Hình thoi có tất cả các tính chất của hình bình hành
+ Các cạnh đối song song và bằng nhau, các góc đối bằng nhau
+ Hai đường chéo giao nhau tại trung điểm mỗi đường.
Ngoài ra còn có
+ Hai đường chéo vuông góc với nhau.
+ Hai đường chéo là các đường phân giác của các góc của hình thoi.
Câu 7: Hãy chọn câu sai
- A
- B
- C
- D
Khẳng định "Tứ giác có hai đường chéo vuông góc với nhau và bằng nhau là hình thoi" sai vì hai đường chéo vuông góc với nhau tại trung điểm mỗi đường mới đảm bảo đủ điều kiện để tứ giác đó là hình thoi
Xem thêm các bài tiếp theo bên dưới