Chiết suất tỉ đối
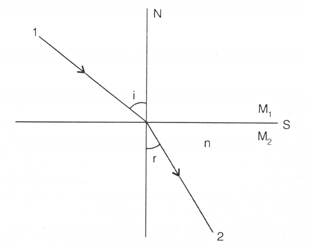
Lý thuyết về Chiết suất tỉ đối
sinisinr=n21⇒sini=nsinr
Trong đó:
i là góc tới; r là góc khúc xạ
n21 là chiết suất tỉ đối của môi trường chứa tía khúc xạ đối với môi trường chứa tia tới.
+ Nếu n21>1 thì góc khúc xạ nhỏ hơn góc tới. Ta nói môi trường (2)
chiết quang kém môi trường (1).
+ Nếu n21<1 thì góc khúc xạ lớn hơn góc tới. Ta nói môi trường (2) chiết quang hơn môi trường (1).
+ Nếu i = 0 thì r = 0: tia sáng chiếu vuông góc với mặt phân cách sẽ truyền thẳng.
+ Nếu chiếu tia tới theo hướng KI thì tia khúc xạ sẽ đi theo hướng IS (theo nguyên lí về tính thuận nghịch của chiều truyền ánh sáng).
Do đó, ta có n21=1n12.
Bài tập tự luyện có đáp án
Câu 1: Chọn phát biểu đúng?
- A
- B
- C
- D
Chiết suất tỉ đối của môi trường 2 so với môi trường 1:
n21=n2n1
+ Nếu n2>n1⇒n21>1
+ Tất cả các môi trường truyền sáng đều có chiết suất không nhỏ hơn 1.
+ Nếu n2<n1⇒n21<1 . Nên chiết suất tỉ đối của hai môi trường có thể nhỏ hơn 1.
Câu 2: Môi trường 2 chiết quang hơn môi trường 1. Hình vẽ nào sau đây mô tả đúng đường đi của tia sáng khi đi từ môi trường 1 vào môi trường 2?
- A
- B
- C
- D
Môi trường 2 chiết quang hơn môi trường 1 nên tia khúc xạ lệch gần pháp tuyến hơn so với tia tới.
Câu 3: Chọn đáp án không đúng?
- A
- B
- C
- D
Chiết suất tỉ đối giữa hai môi trường có thể lớn hơn hoặc nhỏ hơn 1.
Câu 4: Chọn phát biểu không đúng. Chiết suất tỉ đối giữa môi trường chứa tia khúc xạ so với môi trường chứa tia tới được xác định
Chiết suất tỉ đối giữa môi trường chứa tia khúc xạ so với môi trường chứa tia tới được xác định
- A
- B
- C
- D
Chiết suất tỉ đối của 2 môi trường:
n21=n2n1=sinisinr=v1v2
Câu 5: Tốc độ ánh sáng trong chân không là 3.108m/s , chiết suất của xaphia là 1,768. Tốc độ ánh sáng trong xaphia là
- A
- B
- C
- D
Tốc độ ánh sáng trong xaphia: v=cn=3.1081,768=1,7.108(m/s)=170000(km/s)
Câu 6: Chiết suất tỉ đối giữa hai môi trường trong suốt khác nhau có trị số xác định bởi:
- A
- B
- C
- D
Chiết suất tỉ đối của 2 môi trường:
n21=n2n1=sinisinr=v1v2
Câu 7: Cho tia sáng truyền từ môi trường trong suốt này sang môi trường trong suốt khác được mô tả như hình vẽ. Chọn phát biểu đúng? 

- A
- B
- C
- D
Ta có: n2sini=n1sinr
Vì i>r nên sini>sinr⇒n2<n1
Vậy môi trường 1 chiết quang hơn môi trường 2.
Câu 8: Tia sáng đi từ môi trường (1) vào môi trường (2) có dạng như hình vẽ: 
Chọn phát biểu đúng

Chọn phát biểu đúng
- A
- B
- C
- D
Vì tia khúc xạ lệch gần pháp tuyến hơn so với tia tới nên môi trường (2) chiết quang hơn môi trường (1)
Câu 9: Chiết suất tỉ đối giữa môi trường chứa tia tới với môi trường chứa tia khúc xạ:
- A
- B
- C
- D
Chiết suất tỉ đối giữa môi trường chứa tia tới và môi trường chứa tia khúc xạ:
n12=n1n2
Trong đó : n1;n2 là chiết suất của môi trường chứa tia tới và môi trường chứa tia khúc xạ.
Câu 10: Biết chiết suất của một số môi trường tăng dần theo thứ tự nước đá, xaphia, kim cương. Vận tốc của ánh sáng truyền trong các môi trường này được sắp xếp theo thứ tự.
- A
- B
- C
- D
Vận tốc ánh sáng trong môi trường được xác định theo công thức:
v=cn với c là vận tốc ánh sáng trong chân không.
Vậy môi trường nào có chiết suất lớn sẽ có vận tốc nhỏ.
Câu 11: Chiếu ánh sáng từ môi trường A vào môi trường B với góc tới 30o thì thu được góc khúc xạ 45o . Chọn phát biểu đúng?
- A
- B
- C
- D
Ta có: nAsini=nBsinr
Vì i<r⇒sini<sinr⇒nB<nA
Vậy môi trường B có chiết suất nhỏ hơn môi trường A hay môi trường A chiết quang hơn môi trường B.
Câu 12: Chiết suất tuyệt đối của một môi trường truyền ánh sáng
- A
- B
- C
- D
Chiết suất tuyệt đối của môi trường truyền sáng luôn lớn hơn 1.
Câu 13: Tốc độ ánh sáng trong chân không là 3.108m/s, chiết suất của hổ phách là 1,55. Tốc độ ánh sáng trong hổ phách là
- A
- B
- C
- D
Tốc độ ánh sáng trong hổ phách: v=cn=3.1081,55=1,9.108(m/s).
Câu 14: Chiết suất tỉ đối của môi trường 1 đối với môi trường 2 là n12 . Chiết suất tỉ đối của môi trường 2 đối với môi trường 1 là n21 . Biểu thức nào sau đây mô tả đúng mối liên hệ giữa n21 và n12 .
- A
- B
- C
- D
Vì ánh sáng có tính thuận nghịch nên n21=1n12
Câu 15: Chiếu ánh sáng từ môi trường A vào môi trường B với góc tới 30o thì thu được góc khúc xạ 19o . Chọn phát biểu đúng?
- A
- B
- C
- D
Ta có: nAsini=nBsinr
Vì i>r⇒sini>sinr⇒nB>nA
Vậy môi trường B có chiết suất lớn hơn môi trường A hay môi trường B chiết quang hơn môi trường A.
Câu 16: Tốc độ ánh sáng trong một môi trường bằng 23 vận tốc của ánh sáng đó trong chân không. Tìm chiết suất của môi trường đó?
- A
- B
- C
- D
Vận tốc của ánh sáng truyền trong môi trường trong suốt:
v=cn=23c⇒n=32=1,5
Câu 17: Tốc độ ánh sáng trong chân không là 3.108m/s , chiết suất của rượu etylic là 1,36. Tốc độ ánh sáng trong rượu etylic là
- A
- B
- C
- D
Tốc độ ánh sáng trong rượu etylic: v=cn=3.1081,36=2,2.108(m/s)
Câu 18: Chọn phát biểu không đúng.
Chiết suất tỉ đối giữa môi trường chứa tia khúc xạ so với môi trường chứa tia tới được xác định bằng
- A
- B
- C
- D
Chiết suất tỉ đối của 2 môi trường:
n21=n2n1=sinisinr=v1v2
Câu 19: Vận tốc ánh sáng trong các môi trường:
- A
- B
- C
- D
Vận tốc ánh sáng trong môi trường:
v=cn(c=3.108m/s)
Vậy trong các môi trường vận tốc ánh sáng luôn nhỏ hơn vận tốc ánh sáng trong chân không.
Câu 20: Một tia sáng truyền từ môi trường (1) có chiết suất n1 sang môi trường (2) có chiết suất n2 với góc tới i, cho góc khúc xạ r. Tỉ số nào sau đây có giá trị bằng chiết suất tỉ đối n12 của môi trường (1) đối với môi trường (2)?
- A
- B
- C
- D
Ta có: n12=n1n2=1n2n1=1n21