Xét khối chóp S.ABC có đáy là tam giác vuông cân tại A, SA vuông góc v

Xét khối chóp S.ABC có đáy là tam giác vuông cân tại A, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng 3. Gọi $\large \alpha$ là góc giữa hai mặt phẳng (SBC) và (ABC), tính $\large \cos\alpha$ để thể tích khối chóp S.ABC nhỏ nhất

• A.

  A. $\large \cos \alpha=\dfrac{\sqrt{3}}{3}$

   
• B.

  B. $\large \cos\alpha=\dfrac{2}{3}$

• C.

  C. $\large \cos\alpha=\dfrac{1}{3}$

• D.

  D. $\large \cos\alpha=\dfrac{\sqrt{2}}{2}$

Chọn A

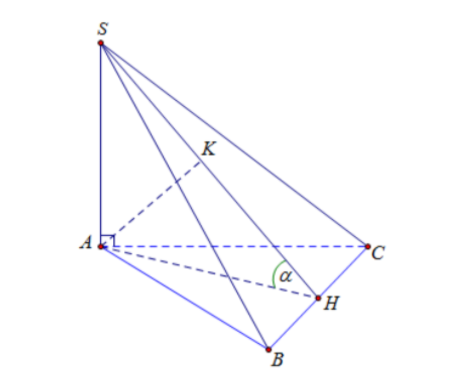
Gọi H là trung điểm của BC $\large \Rightarrow AH\perp BC$ (Vì tam giác ABC vuông cân tại A)

Ta có: $\large \left\{\begin{align}& AH\perp BC\, (cmt)\\& SA\perp BC,\,\, (SA\perp (ABC))$\large \Rightarrow BC\perp (SAH)\Rightarrow BC\perp SH$

Ta có: $\large \left\{\begin{align}& (ABC)\cap (SBC)=BC\\& AH\perp BC\\& SH\perp BC\\\end{align}\right.$ $\large \Rightarrow ((ABC), (SBC))=(AH, SH)=SHA=\alpha$

Kẻ $\large AK\perp SH$ với $\large K\in SH$

Ta có: $\large \left\{\begin{align}& AK\perp SH (gt)\\& AK\perp BC, (BC\perp (SAH))$ $\large \Rightarrow d(A, (SBC))=AK=3$

Tam giác SHK vuông tại K có $\large AH=\dfrac{AK}{\sin \alpha}=\dfrac{3}{\sin \alpha}$

Tam giác SAK vuông tại K có $\large SA=\dfrac{AK}{\sin (90^\circ -\alpha)}=\dfrac{3}{\cos\alpha}$

Tam giác ABC vuông cân tại A có H là trung điểm của BC $\large \Rightarrow BC=2AH=\dfrac{6}{\sin \alpha}$ và $\large AB=AC=\dfrac{BC}{\sqrt{2}}=\dfrac{6}{\sqrt{2}\sin \alpha}$

Vậy $\large S_{ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.\dfrac{6}{\sqrt{2}\sin \alpha}.\dfrac{6}{\sqrt{2}.\sin \alpha}=\dfrac{9}{\sin ^2\alpha}$

$\large V_{S.ABC}=\dfrac{1}{3}.S_{ABC}.SA=\dfrac{1}{3}.\dfrac{9}{\sin^2\alpha}.\dfrac{3}{\cos \alpha}=\dfrac{9}{(1-cos^2\alpha).\cos\alpha}$

Xét hàm số $\large y=(1-\cos^2\alpha).\cos\alpha$ với $\large \alpha\in\left[0; \dfrac{\pi}{2}\right]$

Đặt: $\large t=\cos\alpha\Rightarrow t\in [0; 1]\Rightarrow y=(1-t^2)t=t-t^3$

Suy ra: $\large y'=1-3t^2=0\Leftrightarrow$ $\large \left[\begin{align}& t=\dfrac{\sqrt{3}}{3}\in [0; 1]\\& t=-\dfrac{\sqrt{3}}{3}\notin [0; 1]\\\end{align}\right.$

Ta có: $\large y(0)=0, \,\, y(1)=0, \,\, y\left(\dfrac{\sqrt{3}}{3}\right)=\dfrac{2\sqrt{3}}{9}$ 

Vậy để thể tích khối chóp nhỏ nhất thì $\large (1-\cos^2\alpha}\cos\alpha$ lớn nhất bằng $\large \dfrac{2\sqrt{3}}{9}$ khi $\large \cos \alpha=\dfrac{\sqrt{3}}{3}$