Xét các số phức z thỏa mãn $\large |z+2-i|+|z-4-7 i|=6 \sqrt{2}$. Gọi

Xét các số phức z thỏa mãn $\large |z+2-i|+|z-4-7 i|=6 \sqrt{2}$. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của $\large |z-1+i|$. Tính $large P=m+M$.

 

• A.

  A. $\large P=\sqrt{13}+\sqrt{73}$

• B.

  B. $\large P=\dfrac{5 \sqrt{2}+2 \sqrt{73}}{2}$

• C.

  C. $\large P=5 \sqrt{2}+\sqrt{73}$

• D.

  D. $\large P=\dfrac{5 \sqrt{2}+\sqrt{73}}{2}$

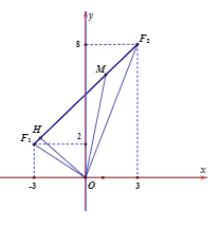
Đặt $\large z-1+i=u \Rightarrow z=u+1-i$, ta cần tìm $\large |u|_{\min }$ và $\large |u|_{\max }$. Thế z vào giả thiết ta có:

$\large |u+3-2 i|+|u-3-8 i|=6 \sqrt{2}$. Gọi M(x;y) biểu diễn u và $\large F_{1}(-3 ; 2), F_{2}(3 ; 8)$ thì ta có $\large \bar{F_{1} F_{2}}=(6 ; 6)$ và $\large M F_{1}+M F_{2}=F_{1} F_{2}=6 \sqrt{2}$, do đó M thuộc đoạn $\large F_{1} F_{2}$. Phương trình $\large F_{1} F_{2}$ là $\large x-y+5=0$, từ đó suy ra

$\large |u|_{min}=O H=d\left(O, F_{1} F_{2}\right)=\dfrac{5 \sqrt{2}}{2} ;|u|_{\max }=O F_{2}=\sqrt{73}$.

Chọn B.