Từ một tấm tôn hình chữ nhật kích thước $\large 50cm\,\, \times\,\, 24

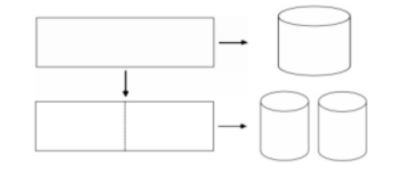
Từ một tấm tôn hình chữ nhật kích thước $\large 50cm\,\, \times\,\, 240cm $, người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau (xem hình minh họa dưới đây):

• Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
• Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.

Kí hiệu $\large V_1$ là thể tích của thùng được gò theo cách 1 và $\large V_2$ là tổng thể tích của hai thùng gò được theo cách 2. Tính tỉ số $\large \dfrac{V_1}{V_2}$

• A. A. $\large \dfrac{V_1}{V_2}=1$
• B. B. $\large \dfrac{V_1}{V_2}=\dfrac{1}{2}$
• C. C. $\large \dfrac{V_1}{V_2}=2$
• D. D. $\large \dfrac{V_1}{V_2}=4$

Chọn C

Ở cách 1, thùng hình trụ có chiều cao h = 50cm, chu vi đáy $\large C_1=240 cm$ nên bán kính đáy $\large R_1=\dfrac{C_1}{2\pi}=\dfrac{120}{\pi}\, (cm)$. Do đó thể tích của thùng là: $\large V_1=\pi.R_1^2h$

Ở cách 2, hai thùng đều có chiều cao h = 50cm, chu vi đáy $\large C_2=120cm$ nên bán kính đáy $\large R_1=\dfrac{C_2}{2\pi}=\dfrac{60}{\pi}$. Do đó tổng thể tích của hai thùng là: $\large V_2=2\pi.R_2^2h$

Vậy $\large \dfrac{V_1}{V_2}=\dfrac{\pi.R_1^2h}{2\pi.R_2^2h}=\dfrac{1}{2}\left(\dfrac{R_1}{R_2}\right)^2=\dfrac{1}{2}.\left(\dfrac{\dfrac{120}{\pi}}{\dfrac{60}{\pi}}\right)^2=2$